数値解析 第13回 (2) 一次変換と固有値・固有ベクトル
一次変換と固有値・固有ベクトル
問 次のネズミの絵を、$2$ 次行列 $\dps{A=\mat{cc}{a & b \\ c & d }}$ を用いた一次変換
$\dps{\mat{c}{x' \\ y'} = A \mat{c}{x \\ y} = \mat{c}{ax+by \\ cx+dy}}$
で変換したらどんな絵になるか?
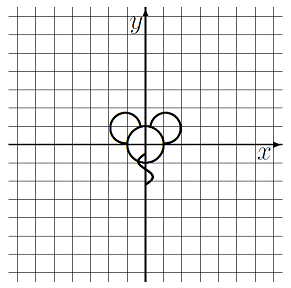
Ex.5 の行列 $\dps{A=\mat{rr}{-3 & 0 \\ 0 & 2}}$ の場合:
$\dps{A\mat{c}{1 \\ 0}=(-3)\mat{c}{1 \\ 0}}$,
$\dps{A\mat{c}{0 \\ 1}=2\mat{c}{0 \\ 1}}$
でした。これは $A$ 倍写像が、
- $x$-軸方向のベクトルを $-3$ 倍し、
- $y$-軸方向のベクトルを $2$ 倍する
ことを意味します。従って、ネズミの絵は
- $x$-軸方向には $3$ 倍して左右を逆転させ、
- $y$-軸方向には $2$ 倍した
絵に写ります。
図のように升目を描けばわかり易いでしょう。
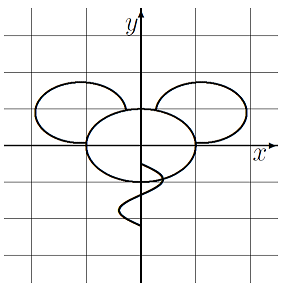
Ex.6 の行列 $\dps{A=\mat{rr}{3 & 1 \\ 1 & 3 }}$ の場合:
$\dps{A\mat{c}{1 \\ 1}=4\mat{c}{1 \\ 1}}$,
$\dps{A\mat{r}{1 \\ -1}=2\mat{r}{1 \\ -1}}$
でした。今度は $A$ 倍写像は
- $\displaystyle{\vvv_1=\mat{c}{1 \\ 1}}$ 方向のベクトルを $4$ 倍し、
- $\displaystyle{\vvv_2=\mat{r}{1 \\ -1}}$ 方向のベクトルを $2$ 倍する
ことを意味します。従って、ネズミの絵は
- $\vvv_1$-方向に $4$ 倍し、
- $\vvv_2$-方向に $2$ 倍した
絵に写ります。
そこで $\vvv_1$ 方向に $X$軸を、$\vvv_2$ 方向に $Y$軸を描いて、$XY$ 座標系で升目を描きましょう。
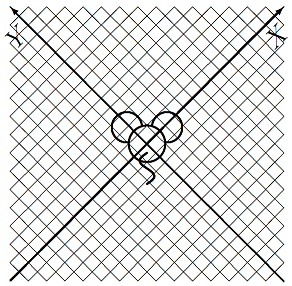
升目を $X$軸方向に4倍、$Y$ 軸方向に2倍して絵を描いたものがネズミの絵の像になります。
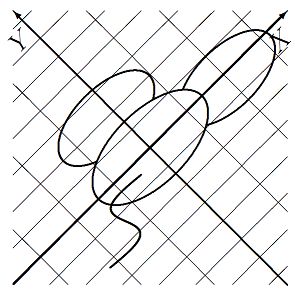
※ このように、$A$ 倍写像の表す一次変換は、固有ベクトル方向に新しい座標系を導入すると分かり易いものになります。
ここ大事!
ネズミの絵がつぶれる場合
のちに説明しますが (
Cor.15 )、$A$ が $0$ 固有値に持つことと、$A$ が逆行列を持つことは同値です。
これをネズミの絵の例で解釈すると、
$0$ が固有値である
$\Leftrightarrow$ $0$ に対する固有ベクトル方向に絵がつぶれてしまう
$\Leftrightarrow$ 絵を元に戻すことができない
$\Leftrightarrow$ $A^{-1}$ が存在しない
ということになります。