組合せとグラフの理論(塩田)第14回 (3) 一般のグラフの完全マッチング
前へ / 戻る / 次へ
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\card}[1]{\left|\,#1\,\right|}$
一般のグラフの完全マッチング
今度は二部グラフに限らず、一般のグラフのマッチングを考えます。
完全マッチングの定義が二部グラフとは異なりますので注意してください。
ここ大事!
Def.12 一般のグラフにおいては、全ての頂点を含むマッチングを「完全マッチング」と呼ぶ。
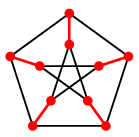
ペテルセングラフは次の定理の代表例です。
Th.14(ペテルセンの定理) 橋を持たない $3$-正則グラフは完全マッチングを持つ。
(証明略)
Rem.15
- 完全マッチングは自動的に最大マッチングでもある。
- 最大マッチングは常に存在するが、完全マッチングは存在するとは限らない。
- 例えば頂点数が奇数なら完全マッチングは存在し得ない。
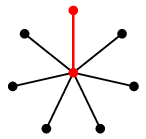
例えば星グラフ $K_{1,n}$ ( $n \geqq 2$ ) の最大マッチングは辺 1 本だけです。
与えられたグラフが完全マッチングを持つかどうかは、
最大マッチングに全ての頂点が含まれるか否か、で判定します。
では、最大マッチングはどうやって求めるのでしょうか。
一般のグラフの最大マッチングアルゴリズム
最大フローアルゴリズムと同様に「増加道」というものが登場します。
Def.16 $M$ を $G$ のマッチングとする。( $M$ はゼロマッチングでもよい。)
このとき、
- $G$ 内の道であって
- $M$ の辺を交互に含み
- 始点と終点がどちらも $M$ に属さないもの
を $M$-増加道と呼ぶ。
Ex.17
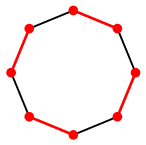
$G$ : 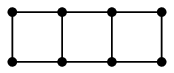
においてマッチング $M$ を
$M$ : 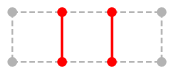
とします。
このとき、次の $P$ や $Q$ は $M$-増加道になります。
$P$ : 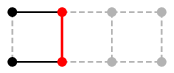 ,
$Q$ :
,
$Q$ : 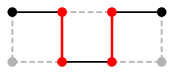
両端が黒い頂点で、辺が交互に黒、赤、黒、赤、$\cdots$ 黒色となる道です。
Prop.18 $P$ が $M$-増加道であれば、辺集合として
$M'=P \oplus M = P$ XOR $M$
とおくことにより、$M'$ は $M$ が辺が 1 本多いマッチングとなる。
$\oplus$ については
第7回の教材 を見てください。
Ex.17 では
$M \oplus P$ : 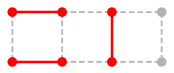 ,
$M \oplus Q$ :
,
$M \oplus Q$ : 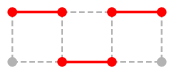
いずれも $M$ より 1 本辺が増えています。
Th.19 $M$ が最大マッチングであること $\Leftrightarrow$ $M$-増加道が存在しないこと。
(証明略)
※ 従って、最大マッチングアルゴリズムには
$M$-増加道を検索するアルゴリズムが必要ですが、
その決定版は Edwards の Blossom アルゴリズム ( 1965年 ) です。
塩田のグラフ描画ツールでも Blossom アルゴリズムを用いて実装していますが、恐ろしく複雑です。
重み付きグラフの最大マッチング
Rem.20
重み付きグラフでは、重みの合計が最大になるようなマッチングを考えることができます。
- たとえば最初の刑事さんの例で、「相性の良さ」を重みとすれば、
相性の良さの合計が最大になるような組み合わせを考えることになります。
- 重み最大マッチングは、辺数最大のマッチングとは異なることがあります。
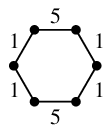 $\Rightarrow$
重み最大マッチングは
$\Rightarrow$
重み最大マッチングは
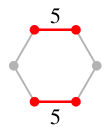
- 郵便配達員問題は、奇数次数の頂点がたくさんあるときは、
重み最大マッチングアルゴリズムを応用して解きます。



 ,
$Q$ :
,
$Q$ : 
 ,
$M \oplus Q$ :
,
$M \oplus Q$ : 
 $\Rightarrow$
重み最大マッチングは
$\Rightarrow$
重み最大マッチングは
