組合せとグラフの理論(塩田)第14回 (2) 二部グラフの完全マッチング
前へ / 戻る / 次へ
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\card}[1]{\left|\,#1\,\right|}$
結婚問題
二部グラフのマッチングは「結婚問題」という観点で述べられます。
結婚問題 適齢期の女性 $m$ 人、男性 $n$ 人のグループがあるとする ( $m \leqq n$ )。
全ての女性がこのグループ内の知り合いの男性と結婚することができるか。
Ex.5 知り合い関係が次の表で表されているとします。
| 女性 | 知り合いの男性 |
| $a$ | $A$, $D$ |
| $b$ | $A$, $C$ |
| $c$ | $B$, $D$, $E$ |
| $d$ | $C$, $E$ |
この関係をグラフで表現すると
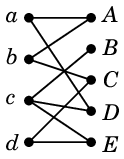
このグラフで次のようなマッチングを取れば全ての女性が知り合いの男性と結婚できます。
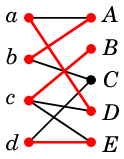
※ 男性が余っていますが、「そこは気にしていない」ことを気に留めておいてください。
Def.6 二部グラフ $G=G(V_1, V_2)$ において、
$V_1$ に属する頂点をすべて含むマッチングを
「$V_1$ から $V_2$ への完全マッチング」と呼ぶ。
結婚問題は $V_1=\{$ 女性 $\}$, $V_2=\{$ 男性 $\}$ としたときに
$V_1$ から $V_2$ への完全マッチングが存在するか、という問題です。
繰り返しますが、二部グラフの完全マッチングでは $V_2$ の頂点は余ってもいいことにします。
ホールの結婚定理
Th.7(ホールの結婚定理) $V_1$ の部分集合 $A$ に対して
$\varphi(A)=\{\,A$ に属する頂点の隣接点たち $\}$
を $A$ の近傍と言う( $\varphi(A)$ は $V_2$ の部分集合である )。
このとき、
$V_1$ から $V_2$ への完全マッチングが存在すること
$\Leftrightarrow$
任意の $A \subseteq V_1$ に対して
$\card{\varphi(A)} \geqq \card{A}$ が成り立つこと $\cdots$ $(\ast)$
証明 $\Rightarrow$) は当然成り立たねばなりません。
$V_1$ から $V_2$ への完全マッチングにおいては、
$A$ の頂点の隣接点はすべて異なるのですから $\card{\varphi(A)} \geqq \card{A}$ となります。
$\Leftarrow$) は次のアルゴリズムを実行します。
Algorithm 8
- 次のようにネットワーク $N$ を作る。
- $G$ の各辺を、$V_1$ から $V_2$ の方向へ向かう重み 1 の弧に置き換える
- 入口 $v$ と出口 $w$ を付加する
- $v$ から $V_1$ の全ての頂点へ、$V_2$ の全ての頂点から $w$ へ、それぞれ重み 1 の弧を作る
 $\longrightarrow$
$N$ :
$\longrightarrow$
$N$ : 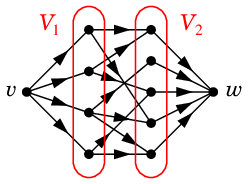
- $N$ の最大フロー $\Phi$ を求める。
$\Phi$ :
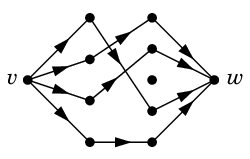
- $\Phi$ から $v$, $w$ を除去し無向化したグラフ $M$ を出力する。
この $M$ が $V_1$ から $V_2$ への完全マッチングになることは次の補題で示します。
Lemma 9 Alg.8 のネットワーク $N$ の最小カットの容量は $\card{V_1}$ に等しい。
従って最大フロー・最小カット定理により
Alg.8 3° の $M$ は $V_1$ から $V_2$ への完全マッチングになる。
証明 $K=(S, \ol{S})$ を任意のカットとすると、
$S$, $\ol{S}$ は次のように分割できます:
$S=\{\,v\,\} \cup X \cup Y$,
$\ol{S}=X' \cup Y' \cup \{\,w\,\}$.
ただし
$X = S \cap V_1$,
$Y = S \cap V_2$,
$X' = \ol{S} \cap V_1$,
$Y' = \ol{S} \cap V_2$.
記号で書くより、次のように図示した方が分かり易いでしょう
(
青い部分が $\require{color}\textcolor{blue}{S}$,
緑が $\textcolor{green}{\ol{S}}$,
赤い弧たちが $\textcolor{red}{K}$ です )。
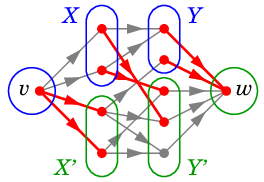
すると $K$ に属する弧は次の 3 種類になります:
- $v$ から $X'$ の頂点に至るもの
- $X$ の頂点から $Y'$ の頂点に至るもの
- $Y$ の頂点から $w$ に至るもの
$N$ の作り方から (i) の弧は $\card{X'}$ 本、(iii) の弧は $\card{Y}$ 本です。
また、$\varphi(X) \cap Y' = \varphi(X) - Y$ の各頂点へは $X$ からそれぞれ 1 本以上の弧がありますので、
(ii) の弧は最小でも $\card{\varphi(X)-Y}$ 本以上あります。
以上から
\begin{align}
K \mbox{ の容量 } &\geqq \card{X'} + \card{Y} + \card{\varphi(X) - Y} \\
&\geqq \card{X'} + \card{Y} + \card{\varphi(X)} - \card{Y} \\
&\geqq \card{X'} + \card{\varphi(X)} \\
&\geqq \card{X'} + \card{X} \quad\qquad (\ \because\ (\ast)\ ) \\
&= \card{V_1} \\
\end{align}
これで、任意のカットの容量が $\card{V_1}$ 以上であることが言えました。
特に $S=\{\,v\,\}$, $\ol{S}=V_1 \cup V_2 \cup \{\,w\,\}$ の場合、
$K=(S,\ol{S})$ は $v$ から $V_1$ の頂点へ至る弧の集合ですからその容量は $\card{V_1}$ であり、
これが最小カットになります。(証明終)
たとえ完全マッチングが存在しないときでも、
$N$ の作り方より次が成り立ちます。
Th.10 $(\ast)$ の成立・不成立に関わらず、
Alg.8 は二部グラフ $G=G(V_1, V_2)$ の最大マッチングを与える。
Rem.11 二部グラフの最大マッチングを求めるアルゴリズムとしては、
もうひとつ、「ハンガリー・アルゴリズム」が有名です。





