数値解析 第5回 (4) 高階微分
高階の中心差分 ( 偶数階 )
$n \geqq 3$ についても $y^{(n)}(x)$ の近似式を作りましょう。
$2$ 階の次は $3$ 階に行きそうですが、偶数を先に考えます
Def.7 $n$ が偶数のとき、$n$ 階の中心差分を再帰的に
( $n$ 階の中心差分 ) = ( $(n-2)$ 階の中心差分 ) の $2$ 階の中心差分
によって定義する。記号で書けば
$\dps{\frac{\delta^n y}{\delta x^n}=\frac{\delta^2}{\delta x^2}\left(\frac{\delta^{n-2} y}{\delta x^{n-2}}\right)}$
( $n=4$, $6$, $\cdots$ )
例えば $n=4$ のとき
$\dps{z=\frac{\delta^2 y}{\delta x^2}}$
として
\begin{align}
\frac{\delta^4 y}{\delta x^4}
&=\frac{\delta^2 z}{\delta x^2} \\
&= \frac{1}{h^2}\{z(x+h) -2\,z(x)+z(x-h)\} \\
&= \frac{1}{h^2}\left[\frac{1}{h^2}\{y(x+2h)-2\,y(x+h)+y(x)\}\right. \\
&\qquad -2\frac{1}{h^2}\{y(x+h)-2\,y(x)+y(x-h)\} \\
&\qquad +\left.\frac{1}{h^2}\{y(x)-2\,y(x-h)+y(x-2h)\}
\right] \\
&= \frac{1}{h^4}\left\{y(x+2h)-4\,y(x+h)+6\,y(x)-4\,y(x-h)+y(x-2h)\right\} \\
\end{align}
といった具合です。
その他の $n$ についてはプリントを見てください:
Rem.8 覚える必要はありませんが、$\dps{\frac{\delta^n y}{\delta x^n}}$ は
- $\dps{\frac{1}{h^n}}$ が掛かります
- $y(x+\frac{n}{2})$, $\cdots$, $y(x-\frac{n}{2})$ が出て来ます
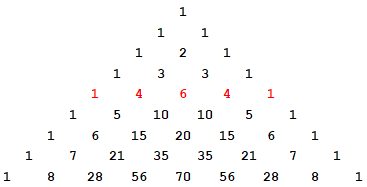
- 係数は、パスカルの三角形の数字に $\pm$ を付けたものです。
たとえば上の $n=4$ の式 は、パスカルの三角形の 4段目の数字 を使います。
高階の中心差分 ( 奇数階 )
Def.9 ( スターリングの公式 ) $n$ が奇数のときは、$n$ 階の中心差分を
( $n$ 階の中心差分 ) = ( $(n-1)$ 階の中心差分 ) の $1$ 階の中心差分
によって定義する。記号で書けば
$\dps{\frac{\delta^n y}{\delta x^n}=\frac{\delta}{\delta x}\left(\frac{\delta^{n-1} y}{\delta x^{n-1}}\right)}$
( $n=3$, $5$, $\cdots$ )
例えば $n=3$ のとき
$\dps{z=\frac{\delta^2 y}{\delta x^2}}$
として
\begin{align}
\frac{\delta^3 y}{\delta x^3}
&=\frac{\delta z}{\delta x} \\
&= \frac{1}{2h}\{z(x+h) - z(x-h)\} \\
&= \frac{1}{2h}\left[\frac{1}{h^2}\{y(x+2h)-2\,y(x+h)+y(x)\}\right. \\
&\qquad -\left.\frac{1}{h^2}\{y(x)-2\,y(x-h)+y(x-2h)\}
\right] \\
&= \frac{1}{2h^3}\left\{y(x+2h)-2\,y(x+h)+2\,y(x-h)-y(x-2h)\right\} \\
\end{align}
といった具合です。証明は略しますが、
Th.10 $n \geqq 3$ のときも、$n$ 階の中心差分の近似誤差は $O(h^2)$ である。