数値解析 第5回 (2) 1階微分
前進差分・後退差分
まずは1階微分の近似式から。
アイデア 微分の定義は
$\dps{y'(x)=\lim_{t \rightarrow 0} \frac{y(x+t)-y(x)}{t}}$
でした。刻み幅 $h \gt 0$ が十分小さければ、$t=h$ として
$y'(x)$ ≒ $\dps{\frac{y(x+h)-y(x)}{h}}$
であろうと考えられます。また $t=-h$ とすれば
$y'(x)$ ≒ $\dps{\frac{y(x-h)-y(x)}{-h}=\frac{y(x)-y(x-h)}{h}}$
とも考えられます。
そこで、$y'(x)$ の近似式として、
Def.1
$\dps{\frac{\mathit{\Delta} y}{\mathit{\Delta} x}=\frac{y(x+h)-y(x)}{h}}$ $\cdots\cdots$ $(1)$
を前進差分 ( 前方差分 )、
$\dps{\frac{\nabla y}{\nabla x}=\frac{y(x)-y(x-h)}{h}}$ $\cdots\cdots$ $(2)$
を後退差分 ( 後方差分 )と呼ぶ。
$h$ を大き目にして誇張して描けば図のようになります:
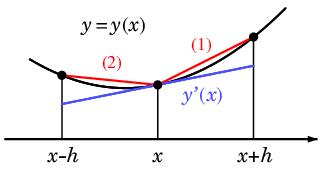 青い線分
青い線分 の傾きが真の $y'(x)$,
赤い線分 (1) の傾きが前進差分、
(2) の傾きが後退差分です。
前進差分・後退差分の誤差評価
Prop.2
$\dps{\frac{\mathit{\Delta} y}{\mathit{\Delta} x}}$, $\dps{\frac{\nabla y}{\nabla x}}$ の近似誤差は、いずれもおおよそ
$\dps{\left|\,\frac{1}{2}y''(x)h\,\right|}$
であり、刻み幅 $h$ の 1 乗オーダー $O(h)$ になる。
証明 $x$ での $y(x)$ のテイラー展開から
$\dps{y(x+h)=y(x)+y'(x)h+\frac{1}{2}y''(x)h^2+O(h^3)}$
従って
$\dps{\frac{\mathit{\Delta} y}{\mathit{\Delta} x}
=\frac{y(x+h)-y(x)}{h}=y'(x)+\frac{1}{2}y''(x)h +O(h^2)}$ $\cdots\cdots$ $(3)$
高次の項 $O(h^2)$ は小さいので、前進差分の誤差は
$\dps{\left|\,\frac{\mathit{\Delta} y}{\mathit{\Delta} x}-y'(x)\,\right|
=\left|\,\frac{1}{2}y''(x)h +O(h^2)\,\right|}$ ≒ $\dps{\left|\,\frac{1}{2}y''(x)h\,\right|}.$
$h$ の代わりに $-h$ を入れた式
$\dps{y(x-h)=y(x)-y'(x)h+\frac{1}{2}y''(x)h^2+O(h^3)}$
からは
$\dps{\frac{\nabla y}{\nabla x}
=\frac{y(x)-y(x-h)}{h}=y'(x)-\frac{1}{2}y''(x)h +O(h^2)}$ $\cdots\cdots$ $(4)$
となって同様です。(証明終)
中心差分
前進差分・後退差分はいまいち精度が良くありません。そこで
次のアイデア $(3)$ と $(4)$ の平均を取ると $y''$ の項が消えます:
$\dps{
\frac{1}{2}\left(
\frac{\mathit{\Delta} y}{\mathit{\Delta} x}
+\frac{\nabla y}{\nabla x}
\right)
=\frac{y(x+h)-y(x-h)}{2h}=y'(x)+O(h^2)}$ $\cdots\cdots$ $(5)$
名前を付けて
Def.3
$\dps{\frac{\delta y}{\delta x}=\frac{y(x+h)-y(x-h)}{2h}}$ を中心差分と呼ぶ。
中心差分は $h$ が多少大きくてもかなり $y'(x)$ に近いことが図からもわかります:
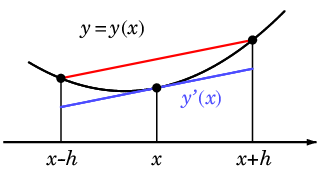 赤い線分
赤い線分 の傾きが中心差分で、多少 $h$ が大きくてもかなり真の $y'(x)$ に近いことが見て取れます。
そして、テイラー展開を $h^3$ の項まで書けば誤差評価ができます。
Prop.4
$\dps{\frac{\delta y}{\delta x}}$ の近似誤差はおおよそ
$\dps{\left|\,\frac{1}{6}y'''(x)h^2\,\right|}$
であり、刻み幅 $h$ の 2 乗オーダー $O(h^2)$ になる。
証明
\begin{align}
y(x+h)&=y(x)+y'(x)h+\frac{1}{2}y''(x)h^2+\frac{1}{3!}y'''(x)h^3+O(h^4) \\
y(x-h)&=y(x)-y'(x)h+\frac{1}{2}y''(x)h^2-\frac{1}{3!}y'''(x)h^3+O(h^4) \\
\end{align}
を辺々引いて
$\dps{y(x+h) - y(x-h)=2y'(x)h+\frac{2}{3!}y'''(x)h^3+O(h^4)}$
$\dps{\frac{\delta y}{\delta x} = \frac{y(x+h) - y(x-h)}{2h}=y'(x)+\frac{1}{3!}y'''(x)h^2+O(h^3)}$
$\therefore$ $\dps{\left| \frac{\delta y}{\delta x} - y'(x) \right| = \left| \frac{1}{3!}y'''(x)h^2+O(h^3) \right| \mbox{≒} \left| \frac{1}{3!}y'''(x)h^2\right|}$

