数値解析 第4回 (4)　スプライン補間
前へ / 戻る / 次へ

3 次スプライン補間

　CG や CAD では 通って欲しい点 をまばらに与えて滑らかな曲線を描きますが、 先程の例で見たとおり、 観測点の間隔が広いときのラグランジュ補間には次のような欠点がありました：
  • 低次のラグランジュ補間は滑らかさに欠ける
  • 高次のラグランジュ補間には不自然な凹凸がある
そこで考え出されたのが
3 次スプライン補間のアイデア　区間 $I_k=[x_k,\,x_{k+1}]$ ごとにひとつずつ 3 次式 $p_k(x)$ を作って、 それらを「上手に」つなぎます。
  1. 区間 $I_k$ の両端では観測値に一致させます：
    $p_k(x_k) = y_k$,   $p_k(x_{k+1}) = y_{k+1}$
  2. 区間 $I_k$ と $I_{k+1}$ のつなぎ目 $x_{k+1}$ では 1 階微分、 2 階微分の値を一致させます：
    $p_k'(x_{k+1}) = p_{k+1}'(x_{k+1})$,   $p_k''(x_{k+1}) = p_{k+1}''(x_{k+1})$

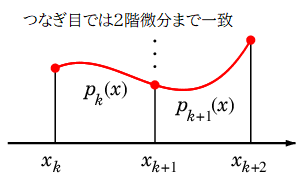
3 次スプライン補間の例

　観測点 $x=0$, $1$, $2$, $3$ に対して観測値を指定して 3 次スプライン補間で曲線を描く Excel ドキュメントも作りました。 次の場所に置いておきます： 黄色のセルの値を書き換えると自動的にグラフも書き換えますので 遊んでみてください。 こんなグラフができます。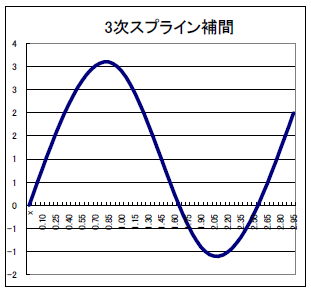

その他の補間法の例

　たとえば、「制御点」を指定して曲線の形を制御する補間法として、 「B-スプライン補間」や「ベジェ曲線」と呼ばれるものがあります。 これらはロボットの軌跡生成などに用いられるそうです。 「組合せとグラフの理論」の教材 の図も、このベジェ曲線を postscript で直書きして描いてあります。

前へ / 戻る / 次へ