数値解析 第6回 (2) 問題設定と基本方針
問題設定
$f(x)$ を、プログラミング言語のライブラリで計算できる関数とし、 定積分 $\dps{\int_a^b f(x)dx}$ の近似値を計算したい、とします。基本方針
今からいくつかの数値積分法を紹介しますが、 共通する基本方針は次のとおりです:- 積分区間 $[\,a,b\,]$ をまず $N$ 等分する。
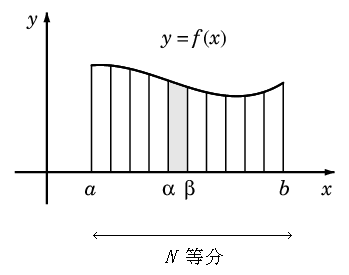
- その $N$ 等分した小区間 $[\,\alpha,\beta\,]$ 内に $m+1$ 個の観測点
$$
\alpha \leqq x_0 \lt x_1 \lt \cdots \lt x_m \leqq \beta
$$
を取り、$x_k$ での観測値を $y_k=f(x_k)$ ( $k=0,1,\cdots,m$ ) とおく。
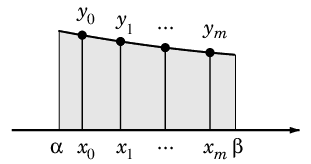
- 観測点 $x_k$ での「重み」$w_k$ を設定し、
$\dps{\sum_{k=0}^m w_k \times y_k}$ $\cdots\cdots$ $(\ast)$ を小区間 $[\,\alpha,\beta\,]$ での積分値 $\dps{\int_{\alpha}^{\beta} f(x)dx}$ の近似値とする。 - $(\ast)$ の値を全ての小区間 $[\,\alpha,\beta\,]$ について足し合わせた値を $\dps{\int_a^b f(x)dx}$ の近似値とする。
設定のいろいろ
-
設定すべき数 $N$, $m$, $x_k$, $w_k$ のうち
- $N$ は実行時に適切に設定します。
- $m$, $x_k$, $w_k$ は各数値積分法で決まっています。
-
$x_k$, $w_k$ の決め方には次のような違いがあります:
- $x_k$ は等間隔に取り、$w_k$ を上手に決める方法:
台形公式、シンプソンの公式、ニュートン・コーツの公式 etc. - $x_k$ と $w_k$ をセットで上手に決める方法:
ガウスの積分公式
- $x_k$ は等間隔に取り、$w_k$ を上手に決める方法: