組合せとグラフの理論(塩田)第11回 (7) 地図の彩色
地図の彩色
Def.16 橋の無い連結平面グラフを「地図」と呼ぶ。
橋の両側は同じ国なので、橋は国境として考えなくていい、という定義です。
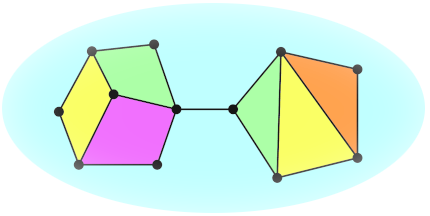
Def.17 地図 $G$ の面に色を割り当て、隣接する面同士は別の色になるようにすることを「G の面彩色」という。
Th.18(四色定理) 全ての地図は 4 色以下で面彩色できる。
( Appel and Haken, 1976)
印刷業者さんの間では経験則として知られていて、提唱されたのは 1852 年。
最初に証明されるまでに 120年 以上が費やされました。
Appel と Haken の証明はコンピュータを用いて「2000個弱の可約配置からなる不可避集合」を作る、というもので、
コンピュータを用いた証明のさきがけでした。
地図の面彩色ではこんなことも言えます。
Th.19 地図 $G$ については、2 色で面彩色できることと、オイラーグラフであることが同値である。
証明 $\Rightarrow)$ ひとつの頂点にはその次数個の面が集まっていますので、
2 色で面彩色できるためには次数は偶数でなければなりません。
$\Leftarrow)$ オイラーサーキットを閉路に分割し、それをベン図だと思って XOR 式に塗り分ければ宜しい。(証明終)