組合せとグラフの理論(塩田)第11回 (6) 平面的グラフの場合
平面的グラフの場合
証明 縮約とは辺を 1 点に潰すことなので、$G$ を平面グラフとして描画しておけば $G'$ にも辺の交差はありません。 (クラトフスキーの定理を使ってもわかります。)(証明終)証明 これも Th.12 と同様に頂点数についての帰納法で示します。
まず 第9回 Cor.19 により、$G$ は次数 $5$ 以下の頂点 $v$ を持ちます。
- $\rho(v) \leqq 4$ のとき
Th.12 と同様に、$G-v$ を $5$ 色以下で点彩色しておけば $v$ に塗れる色が残っています。 -
$\rho(v) = 5$ のとき
$G$ は平面的なので $K_5$ は含みません。 従って $v$ の 5 つの隣接点 $v_1$, $\cdots$, $v_5$ のうち $v_1$ と $v_2$ は隣接しないと仮定できます。 $G$ を $vv_1$, $vv_2$ の 2 辺で縮約したグラフを $G'$ としましょう。 L'a 14 より $G'$ は平面的ゆえ、 帰納法の仮定より 5 色以下で点彩色できます。 そこで $G$ の $v$ 以外の頂点に $G'$ で塗った色を割り当てると、 $v_1$ と $v_2$ は隣接しないのでここまでは点彩色の条件を満たしており、 $v_1$, $\cdots$, $v_5$ には 4 色以下しか使っていませんので $v$ に塗れる色も残っています。(証明終)
正二十面体グラフでは次のようになります。(本当に色を塗ってみました。)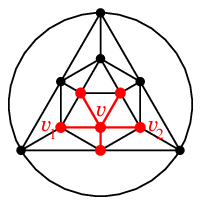
→ 
→ 
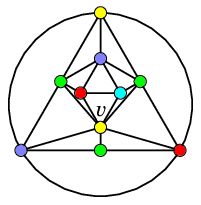
$G$ $G' =G\backslash \{vv_1,vv_2\}$
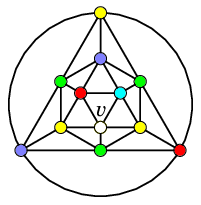
を 5 色で点彩色しておく$v$ には紫が塗れる