組合せとグラフの理論（塩田）第11回 (5) 彩色数の上限についての定理
彩色数の上限についての定理
証明 頂点数についての帰納法で示します。頂点 v を 1 つ取り G′=G−v とおくと、G′ の頂点の次数も ρ 以下ですから 帰納法の仮定により χ(G′)≦ρ+1. です。 そこで、G′ を ρ+1 色以下で点彩色しておくと、 v の隣接点は ρ 個以下なので ρ+1 色のうち v に塗れる色がまだ残っています。(証明終)
例えば次のグラフでは ρ=4 です：
 | → |  | → |  |
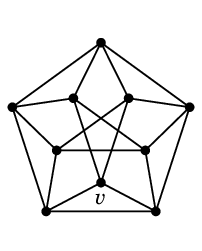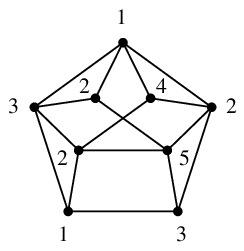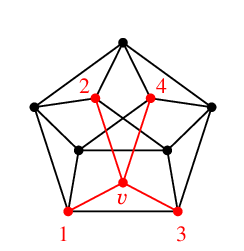| G | G′=G−v を 5 色で点彩色しておく | v には 5 が塗れる |
G が完全グラフでないときはこの上限はあと 1 つ下げることができます。 証明はテキストの §18 にありますが、とても長いので省略します。