組合せとグラフの理論(塩田)第11回 (4) スケジュール調整問題
スケジュール調整問題と彩色問題の関係
問 次の表のように 10 人のメンバー $A,B,\cdots,J$ が6つの委員会 $u,v,\cdots,z$ に
所属しているとする。
各委員にとって会議が重ならないように、最少のコマ数で6つの委員会の時間帯を設定せよ。
| 委員会 | 構 成 員 |
| $u$ | $A$ | $B$ | $C$ | $D$ | $E$ | | | | | |
| $v$ | | | $C$ | $D$ | $E$ | $F$ | $G$ | | | |
| $w$ | | | | | | $F$ | $G$ | $H$ | $I$ | |
| $x$ | | | | | | | | $H$ | $I$ | $J$ |
| $y$ | $A$ | $B$ | | | | | | | | $J$ |
| $z$ | $A$ | $B$ | $C$ | | $E$ | | $G$ | $H$ | $I$ | $J$ |
解 この問題を点彩色を使って解きましょう。グラフを描く訳ですが、まず
とします。では辺は何かと言うと、
「隣接する委員会には違う時間帯を割り振る」
という条件を付けることになるので
ことにします。
例えば $u$ 委員会は、$v$ 委員会とは $C$, $D$, $E$ さんが、
$y$ 委員会とは $A$, $B$ さんが、
$z$ 委員会とは $A$, $B$, $C$, $E$ さんが重なっていますので $v$, $y$, $z$ と隣接させます。
他の委員会についても隣接関係を設定すると次のグラフができます。
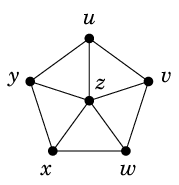
このグラフは $W_6$ ですから彩色数は 4 で、次のように点彩色できます ( 前ページ参照 )。
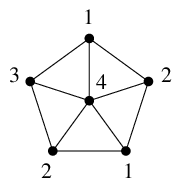
色番号を時間帯と考えて会議は最少では 4 コマで設定できることになります。

