組合せとグラフの理論(塩田)第11回 (3) $K_n$ を含まないのに彩色数が $n$ であるグラフ
$K_n$ を含まないのに彩色数が $n$ であるグラフ<の作り方
彩色数を求める問題は、グラフの中の完全グラフを探す問題とは
違う、
というお話です。
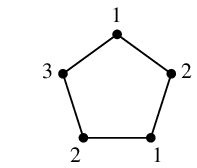
Ex.4 再掲 $C_5$ は $K_3$ を含まないが $\chi(C_5)=3$.
Ex.10 $W_6$ は $K_4$ を含まないが $\chi(W_6)=4$.
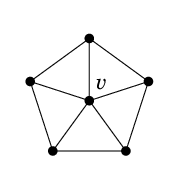
証明 $W_6$ は、$C_5$ に頂点 $v$ をひとつ追加して、$v$ とその他の頂点全てを隣接させたグラフです。
$C_5$ の部分を点彩色するのに 3 色必要で、さらに $v$ にはその 3 色と違う 4 色目が必要となりますので
$\chi(W_6)=4$ になります。
 →
→
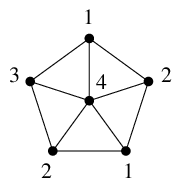
$W_6$ が $K_4$ を含まないことは背理法で示します。
もし $W_6$ が $K_4$ を含んでいると仮定すると、$W_6$ から 1 頂点を除去したグラフには、
$K_4$ から 1 頂点を除去したグラフ $K_3$ が含まれなければなりません。
しかし、$W_6 - v$ は $C_5$ ですから $K_3$ は含みません。(証明終)
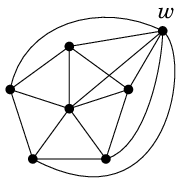
Ex.11 $K_5$ を含まないが $\chi(G)=5$ であるグラフは次のように構成できる。
- $W_6$ に頂点 $w$ をひとつ追加する。
- $w$ とその他の頂点全てを隣接させる。
証明は
Ex.10 と全く同様です。$W_6$ の部分の点彩色に 4 色必要で $w$ には 5 色目が必要。
$G-w$ は $W_6$ ゆえ $G$ が $K_5$ を含むと仮定すると矛盾が生じます。
 →
→
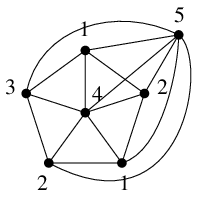
Ex.11 の操作を続けてゆけば、全ての $n \geqq 6$ についても
「$K_n$ を含まないのに彩色数が $n$ であるグラフ」を構成できます。

 →
→

 →
→


 →
→

 →
→
