組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第11回 (2)　基本的命題

前へ / 戻る / 次へ

基本的命題

　基本的な性質を命題としてまとめていきましょう。

Prop.5　

$\chi(G)=1$ であることと、 $G$ が空グラフであることは同値である。
$\chi(G)=2$ であることと、 $G$ が空でない二部グラフであることは同値である。
$T$ が 2 頂点以上の木であれば $\chi(T)=2$ である。
$\chi(K_n) = n$ .
$n \geqq 3$ に対して $\dps{\chi(C_n)=\left\{ \begin{array}{ll} 2 & n \mbox{ が偶数のとき} \\ 3 & n \mbox{ が奇数のとき.} \\ \end{array} \right.}$

証明　

$G$ が空グラフであれば隣接関係が全くないので $\chi(G)=1$ です。辺が 1 本でもあればその両端に違う色を使う必要があるので $\chi(G) \geqq 2$ になります。
$G$ は空でないので $\chi(G) \geqq 2$ であり、次のように 2 色で点彩色できます。
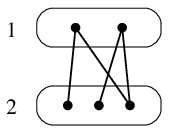
木は二部グラフゆえ。
完全グラフは全ての頂点が互いに隣接していますので、全ての頂点に違う色を使う必要があります。
Ex.4 のように、 $n$ が偶数なら互い違いに塗ればよく、 $n$ が奇数なら 3 色目が必要になります。

(証明終)

部分グラフとの関係

Prop.6　

$H$ をグラフ

$G$ の部分グラフとすると

$\chi(H)$

$\chi(G)$ .

... には

$\leqq$ と

$\geqq$ のどちらが入るでしょうか。

答えは自分で考えてから

Prop.6　

$H$ をグラフ

$G$ の部分グラフとすると

$\chi(H) \leqq \chi(G)$ .

証明　

$G$ を

$\chi(G)$ 個の色で点彩色しておきます。そこからいくつかの頂点と辺を除去すれば

$H$ が得られますが、このとき

$H$ の彩色条件もみたされているので、

$H$ は

$\chi(G)$ 色で点彩色可能です。点彩色可能な色数の最小値が

$\chi(H)$ なので

$\chi(H) \leqq \chi(G)$ です。(証明終)

　平面性の問題では部分グラフの方が描き易かったのと同様、部分グラフの方が束縛条件が少ないので色が塗り易い、ということです。

Prop.7　

$G$ が部分グラフとして

$K_n$ を含んでいれば

$\chi(G) \geqq n$ .

Ex.8　一筆書きでよく使うこのグラフは

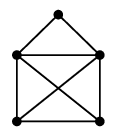
$K_4$ を部分グラフとして含んでいますので彩色数は 4 以上で ( 1° )、実際に次のように 4 色で点彩色できます ( 2° )。

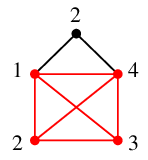
　この例のように Prop.7 は 彩色数の示し方の 1°　に役立つのですが、残念なことに逆が成り立ちません。

Rem.9　

$\chi(G)=n$ であっても

$G$ が

$K_n$ を含むとは言えない。

　従って、

$G$ の含む完全グラフを調べても

$\chi(G)$ は決められません。 ここもとても大事！！

　次の節では Rem.9 のような

$G$ を作って見せます。

前へ / 戻る / 次へ