組合せとグラフの理論(塩田)第11回 (1) 点彩色・彩色数の定義
点彩色の定義
まずは定義から。
Def.1 $G$ をループを持たない無向グラフとする。
$G$ の頂点に色を割り当て、隣接する頂点同士は別の色になるようにすることを「$G$ の点彩色」という。
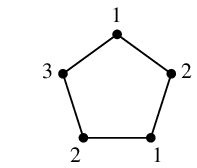
Ex.2 次のグラフに点彩色を施してみましょう。
( 今は色を塗りますが、実際に色を塗るのは大変なので、次からは単に色の番号を振って表します。)
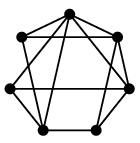
全ての頂点に異なる色を使えば当然点彩色になります。
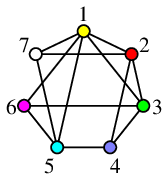
もっと少ない色で点彩色してみましょう。
隣接していなければ同じ色を塗ってもよいので
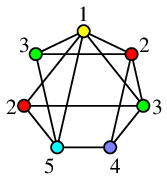 とか
とか
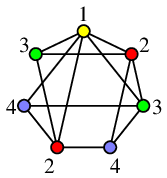
でもOKです。
彩色数の定義
色をたくさん使えば色は塗り易くなります。
しかし
色が多いほどコストは増えます(インクをたくさん買わなければならない、とか)。
そこで、
なるべく使う色を少なくしよう、というのが次の定義です。
Def.3
- $G$ が $k$ 色で点彩色できるとき「 $G$ は $k$-彩色可能である」という。
- $G$ が点彩色できる 最少の色数 を「 $G$ の彩色数」と呼び、$\chi(G)$ と表す。
彩色数の示し方 $\chi(G)=k$ であることを示すには
- $G$ を点彩色するには $k$ 色以上必要であることを示し、かつ
- $G$ が本当に $k$ 色で点彩色できることを示す。
1° は、$G$ が $k-1$ 色以下では点彩色できないことを示すことと同じです。
※ 必要最小限と言わないといけないので 1° を忘れてはいけません。
こことても大事!!
(毎年口を酸っぱくして教えているのですが ... )
Ex.4 $\chi(C_5)=3$.
- 2 色で点彩色しようとすると互い違いに色を使うしかなく、5 つ目の頂点にはどちらの色も使えなくなります。
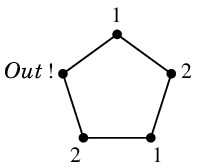
- 次のように塗れば 3 色で点彩色できます。