組合せとグラフの理論(塩田)第7回 (5) 電気回路への応用
電気回路への応用
まずは教科書 p.77 の図を見てください。
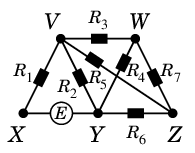
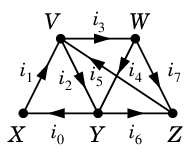
- $R_j$ は各抵抗の抵抗値を表します。
- $i_j$ は各配線の電流量を表します。( 矢印の方向を+とします。)
- $E$ は起電力です。
- 上手に描けていませんが、$VZ$ と $WY$ は交差していないと思ってください。
問題18 $E$ と $R_j$ ( $j=1,2,\cdots$ ) の値を決めたとき、$i_j$ ( $j=1,2,\cdots$ ) の値を求めよ。
この手の問題を解くときに用いるのが
キルヒホフの法則
- 各頂点での電流の総和は $0$ である。
- 各閉路で、電源の電圧の和 $=$ ( 抵抗値 $\times$ 電流量 ) の和、が成り立つ。
(i) は、各頂点で、流入する電流量と流出する電流量が釣り合う、ということです。
(ii) は、電流が抵抗を流れると、( 抵抗値 $\times$ 電流量 ) だけの電圧降下をもたらし、
閉路を一周すると、その電圧降下と供給される電圧が釣り合う、ということです。
Ex.19 3 つの閉路
$C_1=$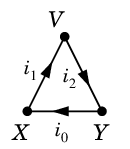 $C_2=$
$C_2=$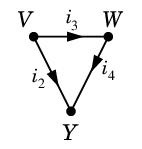 $D=$
$D=$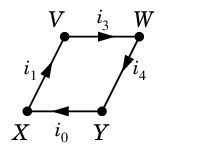
について (ii) 式を書き下すと
$\begin{array}{llll}
C_1 &\!\!\!:&\! R_1i_1 + R_2i_2=E & \cdots\ (1)\\
C_2 &\!\!\!:&\! R_3i_3 + R_4i_4-R_2i_2=0 & \cdots\ (2)\\
D &\!\!\!:&\! R_1i_1 + R_3i_3+R_4i_4=E & \cdots\ (3)\\
\end{array}$
電気回路を表すグラフを $G$ として
Algorithm 20(問題18 の解法)
- $G$ の全域木 $T$ をひとつ求める。
- $T$ に関連した基本閉路集合 ${\cal F}(T)$ を求める。
- (i) の式を各頂点について書く。
- (ii) の式を ${\cal F}(T)$ の各閉路 について書く。(ここ大事!)
- 3-4°の式を $i_j$ たちの連立一次方程式として解く。
(ii) の式を ${\cal F}(T)$ の各閉路についてだけ書けばよい理由は次の命題です。
Prop.21 閉路たちが
$D=C_1 \oplus C_2 \oplus \cdots \oplus C_s$
の関係にあれば
( $D$ についての (ii) 式 ) $=$ ( $C_j$ についての (ii) 式 ) の和
が成り立つ。
任意の閉路は基本閉路の和として表せますので、
その閉路についての (ii) 式は基本閉路についての (ii) 式から自動的に出てくる、という訳です。
Ex.19 では確かに $D=C_1 \oplus C_2$ に従って (3) $=$ (1) $+$ (2) となっていますね。
Rem.22 実際には (i) の式は頂点のうち 1 つだけは省けます。
その理由は、他のすべての頂点で電流の出入りが釣り合っているので、
自動的に最後の頂点でも釣り合ってしまうのです。


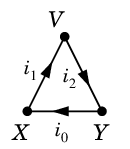 $C_2=$
$C_2=$ $D=$
$D=$