組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第7回 (4)　閉路部分空間 $W(G)$

前へ / 戻る / 次へ

閉路部分空間 $W(G)$

　これもまず定義から。

Def.10　

$G$ 内の閉路たちから

$\oplus$ で作り出せる辺の部分集合全ての集合を

$W(G)$ と表し、「

$G$ の閉路部分空間」と呼ぶ。

$\emptyset$ も

$W(G)$ の要素のひとつとする。

Rem.11　閉路それ自身も全て

$W(G)$ の要素である。

Th.12　

$W(G)$ は

$\mathbb{F}_2$ 上のベクトル空間になる：

加法は $\oplus$
ゼロは $\emptyset$
2倍はゼロなので、スカラーは $\mathbb{F}_2$

証明　Th.7-9 より。

　

$W(G)$ がベクトル空間になることがわかりましたので、あとは「基底ベクトル」をみつけさえすれば

$W(G)$ 内の全てのベクトル、特に

$G$ の全ての閉路を統制できることになります。

基本閉路集合

Def.13　

$G$ を連結グラフ、

$T$ をその全域木のひとつとする。

$T$ に属さない

$G$ の辺

$e$ を

$T$ に付加すると閉路

$C_e$ が 1 つだけできる（第6回 Th.5）。そのような

$C_e$ 全ての集合を

${\cal F}(T)$ と表し、「

$T$ に関連した基本閉路集合」と呼ぶ。

Ex.14　Ex.6 と同じグラフ

$G=$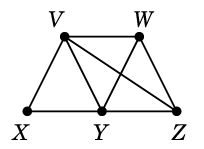

において、全域木

$T=$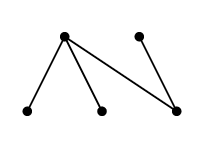

を選んだとしましょう。このとき

$T$ に属さない辺は次の

$e$ ,

$f$ ,

$g$ ,

$h$ の 4 本です。

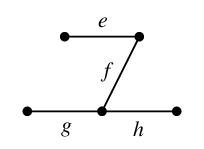
$T$ に

$e$ を付加すると、次のように閉路でき（赤い部分）、これが

$C_e$ です。

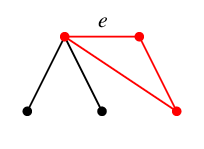
同様に

$T$ に

$f$ を付加してできる閉路が

$C_f$ ,

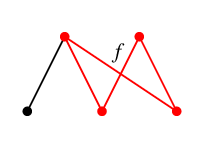
$T$ に

$g$ を付加してできる閉路が

$C_g$ ,

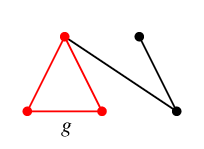
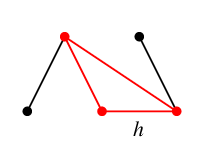
$T$ に

$h$ を付加してできる閉路が

$C_h$ です。

結局、

$T$ に関連した基本閉路集合

${\cal F}(T)$ は


$C_e$	$C_f$	$C_g$	$C_h$

となります。

Th.15　

${\cal F}(T)$ は

$W(G)$ の基底になる。すなわち

全ての閉路は、基本閉路と $\oplus$ で作ることができる。ここが肝心!!
$\dim W(G) = m - n + 1$ .　（ただし、 $G$ の頂点数を $n$ , 辺数を $m$ とする。）

証明　(1)　基本閉路

$C_e$ ,

$C_f$ ,

$\cdots$ を係数 1 で足し合わせると、

$C_e \oplus C_f \oplus \cdots = \{\,e,f,\cdots\,\} \neq \emptyset$ であり、これは基本閉路たちが一次独立であることを意味しています。そして、任意の閉路

$C$ は次のアルゴリズム Alg.16 によって基本閉路の和として表すことができます。

(2)　次元とは基底ベクトルの個数のことであり、それは $T$ に属さない $G$ の辺の本数でしたから

$\dim W(G) =$ (

$G$ の辺数 )

$-$ (

$T$ の辺数 )

$=m - (n - 1)$ . (証明終)

閉路を基本閉路の和に表すアルゴリズム

Algorithm 16

入力： $G$ の閉路 $C$
出力： $C$ を基本閉路の和として表す表し方

$T$ に属さない $C$ の辺を $e$ , $f$ , $\cdots$ , $h$ とする。
$C_e \oplus C_f \oplus \cdots C_h$ を出力する。

証明　

$D=C_e \oplus C_f \oplus \cdots C_h$ とおくと、

$e$ ,

$f$ ,

$\cdots$ ,

$h$ は全て

$C$ と

$D$ に 1 回ずつ含まれますので、

$C \oplus D$ には含まれません。すなわち

$C \oplus D$ は

$T$ の辺の部分集合になります。 Th.5 から

$C \oplus D$ は閉路に分けられるはずですが、木

$T$ は閉路を含みませんので、結局

$C \oplus D=\emptyset$ .　よって

$C = -D = D$ . (証明終)

Ex.17　Ex.14 の状況

$G=$

$T=$

では

$W(G)$ の次元は

$4$ で、


$C_e$	$C_f$	$C_g$	$C_h$

が

$W(G)$ の基底です。その要素は

$\emptyset,\quad C_e,\quad C_f,\quad C_g,\quad C_h,$

$C_e \oplus C_f,\quad C_e \oplus C_g,\quad C_e \oplus C_h,\quad C_f \oplus C_g,\quad C_f \oplus C_h,\quad C_g \oplus C_h,$

$C_e \oplus C_f \oplus C_g,\quad C_e \oplus C_f \oplus C_h,\quad C_e \oplus C_g \oplus C_h,\quad C_f \oplus C_g \oplus C_h$

$C_e \oplus C_f \oplus C_g \oplus C_h$ の 16 個となります。

　Alg.16 を実行してみましょう。入力を

$C=$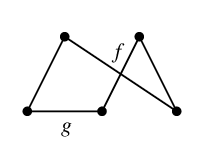

とします。このとき

$T$ に属さない

$C$ の辺は

$f$ ,

$g$ の 2 本です。

$C_f=$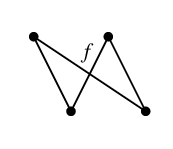

と　

$C_g=$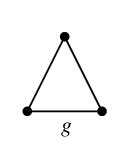

を重ねて描くと

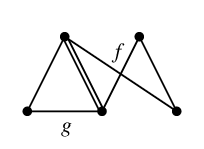
二重辺を消して

$C_f \oplus C_g=$

$C$ になりましたね。

やってみよう　Ex.17 の状況で、今度は

$C'=$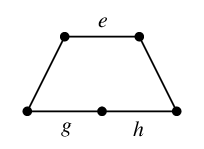

を入力として Alg.16 を実行してみましょう。

答え

$T$ に属さない

$C'$ の辺は

$e$ ,

$g$ ,

$h$ の 3 本です。

$C_g=$

$C_h=$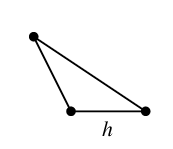

$C_e=$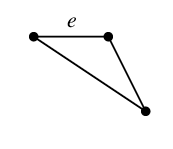

を重ねて描くと

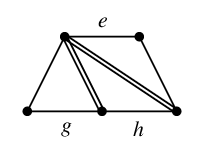
二重辺を消して

$C_e \oplus C_g \oplus C_h=$

$C'$ になりましたね。

前へ / 戻る / 次へ