組合せとグラフの理論（塩田）第5回 (4)　有向グラフのオイラー性
前へ / 戻る / 次へ

有向グラフのオイラー性

　有向グラフでは弧の向きに従って一筆書きを考えます。 （一方通行が指定されている道路をイメージしてください。）
Def.16　有向グラフの頂点 $v$ に対し、その入出次数とは
  • 入次数 $\mbox{indeg}(v)=$ ( $v$ に入る弧の本数 )
  • 出次数 $\mbox{outdeg}(v)=$ ( $v$ から出る弧の本数 )
では
$\mbox{indeg}(v)=1$, $\qquad\mbox{outdeg}(v)=2$
と数えます。
Th.17　連結な有向グラフ $D$ について
$D$ がオイラーグラフであること
$\qquad\Leftrightarrow$ $D$ のすべての頂点 $v$ で $\mbox{indeg}(v)=\mbox{outdeg}(v)$ が成り立つこと
証明 は無向グラフの場合を若干修正すればできます。ポイントは
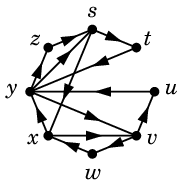
  • 有向オイラーサーキットは有向閉路に分けられること
  • 有向閉路では $\mbox{indeg}(v)=\mbox{outdeg}(v)=1$ が成り立つこと
  • Alg.5, Alg.6 は向きを指定しても成り立つこと
です。

前へ / 戻る / 次へ