組合せとグラフの理論（塩田）第5回 (3) ハミルトン性
定義
今度は、全ての
頂点 を含む道、あるいは閉路を持つかどうかを考えます。
Def.12 オーダー $n$ のグラフ $G$ について、
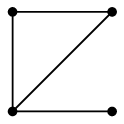
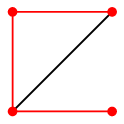
- $P_n$ と同型な部分グラフを持つとき（すなわち全ての頂点を通る道を含むとき）、
$G$ を半ハミルトングラフと言う。
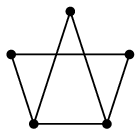
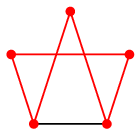
- $C_n$ と同型な部分グラフを持つとき（すなわち全ての頂点を通る閉路を含むとき）、
$G$ をハミルトングラフと言う。
それぞれ、その部分グラフを半ハミルトン道、ハミルトンサイクルと呼ぶ。
例と注意
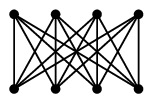
Ex.13 次のグラフはハミルトングラフでしょうか？
-
答え
赤い部分グラフが半ハミルトン道です。
しかし、右下の頂点を含む閉路は存在しないのでハミルトングラフではありません。
-
答え
赤い部分グラフがハミルトンサイクルです。
-
答え
立方体グラフもハミルトングラフです。
-
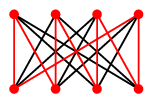
答え
$K_{n,n}$ ( $n \geqq 2$ ) もハミルトングラフです。
ちなみに、
$K_{n,n+1}$ ( $n \geqq 1$ ) は半ハミルトンですが、
$K_{n,n+k}$ ( $n \geqq 1$, $k \geqq 2$ ) は半ハミルトンにもなりません。
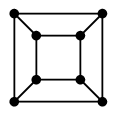
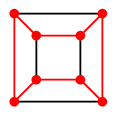
Ex.14 次のグラフも全てハミルトングラフです。
- $C_n$ ( $n \geqq 3$ )
- $K_n$ ( $n \geqq 3$ )
- プラトングラフたち
- $Q_k$ ( $k \geqq 2$ )
Rem.15
- ハミルトン性の判定は NP 完全問題ですので、高速なアルゴリズムはありません。
（オイラー性の判定が、次数を数えるだけなので瞬時にできることと対照的です。）
- テキスト Th.7.1 は
「やたらたくさん辺があればハミルトングラフである」
という内容ですが、仮定が強すぎるので実社会ではほとんど使えません。
- オイラー性は郵便配達員問題に、ハミルトン性は巡回セールスマン問題に関わっています。詳しくは後日。
