組合せとグラフの理論(塩田)第5回 (2) もうひとつのアルゴリズム
フルーリーのアルゴリズム
オイラーサーキットを求めるもうひとつのアルゴリズムがあります:
Algorithm 10 ( Fleury ) オイラーグラフ $G$ のオイラーサーキットは次の手順で求まる:
- テキトーな頂点から出発する。
- 現在地の接続辺を 1 つ選んで進む。ただし、橋は、他にたどるべき辺がないときだけ選んで良い。
- たどった辺は除去し、孤立点も除去する。
- 辺が無くなれば終了。そうでなければ 2°へ。
Ex.11 Ex.7 と同じグラフで
Alg.10 を実行してみましょう。
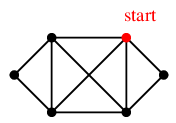
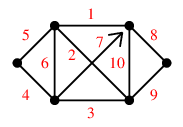
右上の頂点から出発して図のように進んだとします。
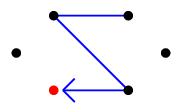
たどった辺( 青い辺 )を除去すると、残った辺は次の通りです。
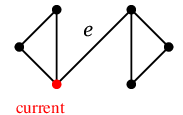
現在地( 赤い頂点 )には橋 $e$ が接続していますが、他にもたどれる辺があるので、$e$ は渡らず左の三角形へ進みます。
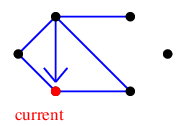
たどった辺を除去し、孤立点も除去します。すると現在地には $e$ しか接続辺が無いので、今度は $e$ へ進みます。
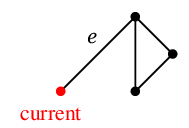
一筆書きの道順はこのようになりました。
プログラミング上の注意
-
Alg.6 には
- 閉路を 1 つ見つけるルーチン Alg.5
- 連結成分へ分解するルーチン
が必要で、また、再帰的アルゴリズムのデメリットとして、メモリを大量に消費します。
-
Alg.10 は
があれば実装できます。塩田のツールでは Alg.10 を用いています。
- 連結成分への分解、橋の判定は、後日勉強する幅優先探索・深さ優先探索を応用して行います。