組合せとグラフの理論(塩田)第5回 (1) オイラー性
定義と例
特に断りがないときは、今日扱うグラフは全て連結であるとします。
Def.1
- 一筆書きができる無向グラフを半オイラーグラフと呼ぶ。
- 一筆書きで 出発点へ戻れる 無向グラフをオイラーグラフと言い、その道順をオイラーサーキットと呼ぶ。
Ex.2
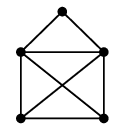
一筆書きの例として有名なグラフですが、このグラフでは出発点へ戻る一筆書きはできません。
すなわち、このグラフは半オイラーグラフですが、オイラーグラフではありません。
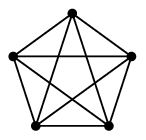
$K_5$ はオイラーグラフです。
一つの頂点からまず外側の五角形を書いて、次に内側の星を書けばOKです。
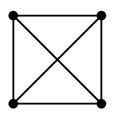
$K_4$ はただの一筆書きもできません。すなわち半オイラーグラフですらありません。
※ それぞれ確かめてみましょう。
定理
次の定理は第1回の授業でも紹介しました:
Th.3 連結な無向グラフ $G$ について
$G$ がオイラーグラフであること $\Leftrightarrow$ $G$ のすべての頂点の次数が偶数であること
※ オイラー性はグラフ全体についてのグローバルな性質ですが、
それが次数というローカルな性質で言い換えられるというのはとても興味深いことです。
※ オイラー先生は「オイラーグラフであれば全ての次数は偶数である」ことを示し、
その対偶から橋渡りが不可能であることを導きました。
十分条件の「全ての次数が偶数ならばオイラーグラフである」ことを示したのは後の研究者
ヒールホルツァーだと言われています。
証明
Lemma 4 $G$ のすべての頂点の次数が 2 以上であれば、$G$ には閉路が含まれる。
構成的証明 次のアルゴリズムを実行すれば良い。
Algorithm 5
- テキトーな頂点から小道を作り始める。
- 来た辺へは戻らずに先へ進み続ける。
(これは任意の頂点の次数が 2 以上なので可能です。)
- 訪問回数が 2 回になった頂点ができた時点で次のような閉路ができる。
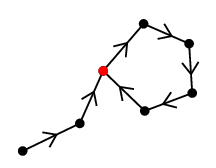
Th.3 の構成的証明 $\Rightarrow$ ) オイラーサーキットは閉じた小道ですから、
第4回の
Prop.3 により閉路に分割することができます。
閉路ではすべての頂点の次数は 2 なので、
それらを重ね合わせてできるグラフの頂点の次数は偶数になります。
$\Leftarrow$ ) 次のアルゴリズムを実行します:
Algorithm 6
- Alg.5 を用いて閉路 $C_0$ を見つける。
- $G-C_0$ の連結成分を
$G_1$, $G_2$, $\cdots$, $G_k$
とする。
- 各 $G_j$ は全ての頂点の次数が偶数である連結グラフゆえオイラーグラフになる。
そこで(再帰呼び出しにより)$G_j$ のオイラーサーキット$C_j$ を求る。
- $C_0$ と $C_j$ の交点の一つを $v_j$ とする。
- $C_0$ 上の 1 点 $v_0$ から $C_0$ をたどり、
$v_j$ へ来たら $C_j$ を迂回してから先へ進む。
Ex.7 図のグラフ $G$ で
Alg.6 を実行しましょう。
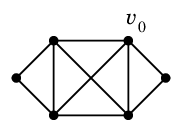
$v_0$ からまず
Alg.5 を実行して次の閉路 $C_0$ が得られたとします。
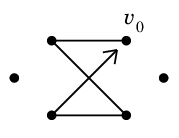
$G-C_0$ の連結成分は 2 つあり、それぞれ図のようなオイラーサーキット $C_1$, $C_2$ を持ちます。
$C_1$ と $C_0$ の交点 $v_1$,
$C_2$ と $C_0$ の交点 $v_2$ を取ります。
$C_1$
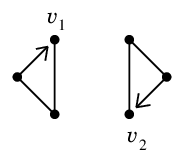 $C_2$
$C_2$
5°に従って次のオイラーサーキットを得ます。
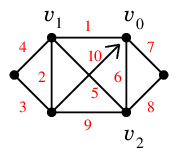
Cor.8 連結な無向グラフ $G$ について
$G$ がオイラーグラフでない半オイラーグラフであること
$\Leftrightarrow$ $G$ には奇数次数の頂点が丁度 2 個あること
証明は次の例を見ればわかるでしょう:
Ex.9 $K_{2,3}$ では、図の $u$, $v$ が奇数次数です。
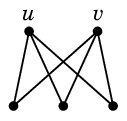
$K_{2,3}$ に辺 $e=uv$ を付加するとすべての頂点の次数が偶数になってオイラーグラフになります。
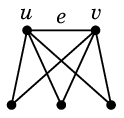
そのオイラーサーキットを求めて、そこから $e$ を取り除けば $K_{2,3}$ の一筆書きになります。






 $C_2$
$C_2$


