組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第4回 (2)　命題ひとつ

命題ひとつ

　次の命題は次回の一筆書きに使います：

Prop.3　閉じた小道

$T$ は閉路に分割できる。

Ex.4　例えば次のグラフの赤線のような閉じた小道

$T$

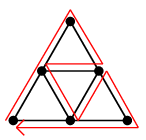
は

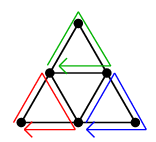や

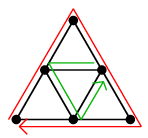
のように分けることができます。 ( 一通りとは限りません。)

Prop.3 の構成的証明　

$T$ を

$T:v_0 \rightarrow v_1 \rightarrow \cdots \rightarrow v_n$ とし、

$v_0$ から出発して訪問回数が最初に2回になる頂点を

$v_i = v_j$ 　(

$i \lt j$ ) とします (

$v_n=v_0$ なのでこのような頂点が必ずあります ) 。このとき、

$C:v_i \rightarrow v_{i+1} \rightarrow \cdots \rightarrow v_j$ は

$T$ に含まれる閉路になります。

$T$ から

$C$ を取り除いて

$\require{color}$

$T':v_0 \rightarrow \cdots \rightarrow \textcolor{red}{v_i \rightarrow v_{j+1}} \rightarrow \cdots \rightarrow v_n$ という歩道

$T'$ を作ると、これは

$T$ より短い閉じた歩道になります。（

$v_i=v_j$ なので

$v_i$ と

$v_{j+1}$ は隣接しています。）帰納法の仮定より

$T'$ は閉路に分割できるので、それらと

$C$ と合わせれば宜しい。(証明終)

　Ex.4 では図の赤い頂点が最初に訪問回数が2回になります。

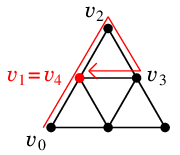
従って

$C$ ,

$T'$ は

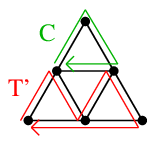
となります。

$T'$ に対して「構成的証明」を再帰的に適用すると図の閉路

$C'$ がみつかり、

$T'$ から

$C'$ を取り除いた

$T''$ が閉路になっているので、これで分割が終了します。

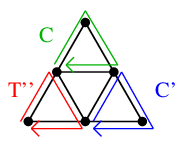
プログラミングのために大切なこと　