組合せとグラフの理論（塩田）第4回 (3) 道を用いた連結性の定義
連結性の定義
Def.5 グラフ $G=(V,E)$ が連結である、とは、任意の2頂点 $u$, $v \in V$ に対して $u$-$v$ 道が存在すること。
これは第3回の
Def.5 の言い換えになっています。
Th.6 $V$ 上の関係 $\sim$ を
$u \sim v$ $\Leftrightarrow$ $u$-$v$ 道が存在すること
と定めれば、$\sim$ は同値関係であり、
$\sim$ による類別が $G$ の連結成分を与える。
Ex.7 次のグラフ
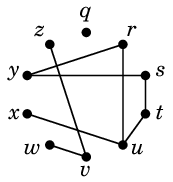
では
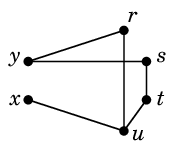
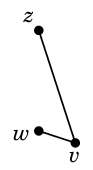
$r \sim s \sim t \sim u \sim x \sim y$, $v \sim w \sim z$
となっていて、3つの連結成分が得られます：
復習
- 同値関係とは「同じ」ということの論理的表現で、次の3つの条件を満たす関係でした：
- 対称律：$a \sim a$
- 反射律：$a \sim b$ $\Rightarrow$ $b \sim a$
- 推移律：$a \sim b$ かつ $b \sim c$ $\Rightarrow$ $a \sim c$
- 同値なもの同士をひとつのクラス（$=$ 同値類）として分類することが、同値関係の大きな目的です。
- 小学校から習ってきた同値関係として次のようなものがあります：
- 図形の合同関係
- 図形の相似関係
- 整数の合同関係 $x \equiv y \pmod n$
二部グラフの特徴付け
次の定理は、「二部グラフ」という構造を「閉路」を用いて特徴付けます：
Th.8 単純無向グラフ $G$ について次は同値である：
- $G$ が二部グラフであること
- $G$ の任意の閉路が偶数長であること
証明 (1) $\Rightarrow$ (2)
閉路を作るためには2つの頂点集合を数回往復しなければならないので。
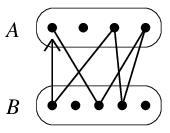
(2) $\Rightarrow$ (1)
$G=(V,E)$ の各連結成分が二部グラフであれば $G$ 全体も二部グラフになるので、
以下、$G$ が連結であると仮定して証明します。頂点 $u \in V$ をひとつ固定し、
$A=\{\,v \in V \,|\, $ 最短の $u$-$v$ 道は偶数長 $\,\}$
$B=\{\,v \in V \,|\, $ 最短の $u$-$v$ 道は奇数長 $\,\}$
とおきましょう。$G$ は連結なので $V=A \cup B$ となっています。
$A$ の頂点同士、$B$ の頂点同士は隣接しないことを示します。
もし $A$ の2頂点 $v$, $w \in A$ が隣接すると仮定すると、
最短の $u$-$v$ 道、最短の $u$-$w$ 道と辺 $vw$ の絵はこのような状態になっています：
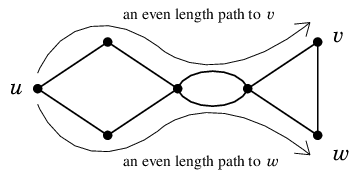
合計で奇数本の辺が描かれていることに注意してください。
ここから二重辺を除去すると
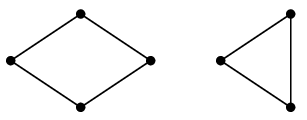
のようにいくつかの閉路が残りますが、辺の本数が奇数ですから、
その中に奇数長の閉路が存在することになり仮定に矛盾します。
$B$ の2頂点 $v$, $w \in B$ が隣接すると仮定しても同様の矛盾が生じますので、
$G$ が二部グラフであることが示されました。(証明終)
Cor.9 二部グラフは部分グラフとして $C_3$ ( 三角形 ) を含まない。
第２回の
Ex.10 では
$G=$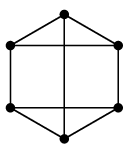
と
$H=$
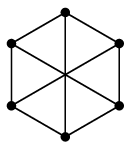は同型ではない
と言いましたが、$H$ は完全二部グラフ $K_{3,3}$ と同型なので三角形を含まない、
というところが要
(かなめ)でした。