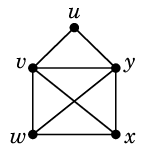
組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第4回 (1)　グラフの中の道いろいろ

定義

　まず、いろいろな種類の道を定義して、そのあとで例を示します。

Def.1

(1)　歩道 ( walk )

隣接する頂点を次々辿ってゆく道筋を「歩道」と呼ぶ。（辿り方には特に制限はありません。） $v_0 \rightarrow v_1 \rightarrow \cdots \rightarrow v_n$ $v_0$ を始点、$v_n$ を終点と呼ぶ。

(2)　小道 ( trail )

同じ辺は二度通らない歩道のこと。同じ頂点を通ることは許す。

(3)　閉じた小道

始点と終点が等しい小道は「閉じた小道」と呼ぶ。

(4)　道 ( path )

今後、単に「道」と言えば、同じ点を二度通らない小道を指すこととする。ただし、始点と終点が等しいことだけは許す。始点が $v$, 終点が $w$ である道は「$v$ から $w$ へ至る道」、「$v$-$w$ 道」などと呼ぶ。

(5)　閉路 ( cycle )

閉じた道を特に「閉路」と呼ぶ。つまり

※　なお、教科書によって微妙に用語が違うことがありますので、読んでいておかしいときはその本の定義を見直してください。

例

Ex.2　次のグラフ

の中でいろいろな歩道を見てみましょう。

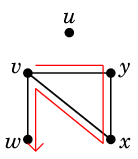		これは (1) の記号で　　$v \rightarrow y \rightarrow x \rightarrow v \rightarrow w$ と書ける歩道です。同じ辺は通っていませんので小道ですが、中間で $v$ を二度通っているので道ではありません。
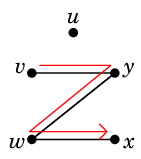		これは道です。
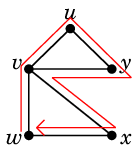		これは閉じた小道ですが、閉路ではありません。中間点 $v$ を２度通っています。
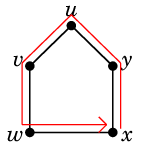
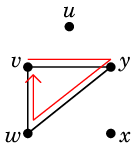
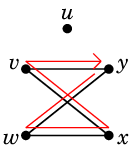これらは閉路です。