組合せとグラフの理論(塩田)第9回 (4) 交差数と厚さ
交差数 $\mbox{cr}(G)$ と厚さ $\mbox{t}(G)$
非平面的グラフについて、それがどのくらい平面的から遠いかを数で表しましょう。
Def.20
- $G$ を平面上に描くときに生じる辺の交差の最小数を「$G$ の交差数」と呼び、$\mbox{cr}(G)$ と表す。
- $G$ ( の辺 ) をいくつかの平面的な部分グラフに分ける最小数を「$G$ の厚さ」と呼び、$\mbox{t}(G)$ と表す。
Rem.21
- $G$ が平面的 $\Leftrightarrow$ $\mbox{cr}(G)=0$ $\Leftrightarrow$ $\mbox{t}(G)=1$
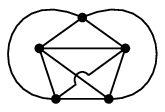
- $K_5$ は非平面的ですから交差数は 1 以上ですが、図のように交差1 つで描画できますので $\mbox{cr}(K_5)=1$ です。
- また $K_5$ は次のように 2 つの平面的部分グラフに分けられますので $\mbox{t}(K_5)=2$ です。
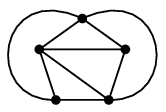
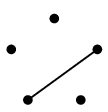
- この例のように、交差する辺を 1 つずつ別の部分グラフに割り当てることで
$\mbox{t}(G) \leqq \mbox{cr}(G)+1$ であることがわかります。
※ 交差数は立体交差をイメージすればよく、
厚さの方は「電気回路が何層で設計できるか」と想像すれば覚えられるでしょう。