組合せとグラフの理論（塩田）2023年度

組合せとグラフの理論（塩田）第9回 (3)　オイラーの公式

前へ / 戻る / 次へ

「面」の定義

　平面グラフに「面」を定義するために、ひとつ定理を書きます。

Th.14　グラフが平面上に辺の交差無く描けることと、球面上に辺の交差無く描けることは同値である。

証明　

$\Rightarrow$ )　小さな紙に描いておいて球面に張り付ければよい。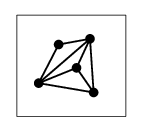

　→　

$\Leftarrow$ )　グラフを避けて球面に穴をあけて、穴を広げればよい。

　→　

(証明終)

Rem.15　

Th9-10 の証明は、球面上に描くと思えば内側外側の区別が不要になります。
プラトングラフの平面グラフとしての描画 ( Ex.5 ) は、正多面体の面のひとつに穴をあけて広げたものです。

Def.16　平面グラフの、辺で区切られた各領域を「面」と呼ぶ。一番外側も 1 つの面と考える。

※　球面上に描けば「一番外側」という区別がなくなるので、その面も同等に扱う訳です。
※ 「面」と言うときは 辺が交差していないことが前提 です。 ここ特に大事！！

オイラーの公式

Th.17（オイラーの公式）　

$G$ を連結な平面グラフ、

$n$ ,

$m$ ,

$f$ をその頂点数、辺数、面の個数とする。このとき

$n - m + f = 2$ が成り立つ。

Ex.18　プラトングラフで確かめてみましょう。

答え

	$n$	$m$	$f$	$n-m+f$
正四面体グラフ	4	6	4	2
立方体グラフ	8	12	6	2
正八面体グラフ	6	12	8	2
正十二面体グラフ	20	30	12	2
正二十面体グラフ	12	30	20	2

$n$ ,

$m$ ,

$f$ の値が対称に並んでいる理由は次回勉強します。

Th.17 の証明　

$m$ についての帰納法を用います。

$m$ が一番少ないのは $G$ が木のときで $m=n-1$ であり、面は外側のひとつだけなので $f=1$ 。よって $n-m+f = n - (n-1) + 1= 2$ となって成り立ちます。
G が木でないときは、G 内の閉路 C と、C 上の辺 e を 1 本選んで $G'=G-e$ を考えます。G′ は G の部分グラフゆえ平面グラフで、そのパラメータを n′, m′, f′ とおくと
- 頂点は消していないので $n'=n$
- 辺は 1 本除去したので $m'=m-1$
- $e$ の表側の 2 つの面が 1 つにつながったので $f'=f-1$
よって $n-m+f=n'-(m'+1)+(f'+1)=n'-m'+f'=2$ . ここで G′ に帰納法の仮定を使いました。(証明終)

平面的グラフは辺が少ない

Cor.19　

$G$ を連結な平面的単純グラフ、

$n$ ,

$m$ をその頂点数、辺数とする。このとき次が成り立つ。

$m \leqq 3n-6$ .
$G$ が3角形を含まなければ $m \leqq 2n-4$ .
次数 5 以下の頂点が必ずある。

証明　(1)　1 つの面は 3 本以上の辺で囲まれていて、1 本の辺は 2 つの面で使われますので、

$3f \leq 2m$ が成り立ちます。従って

$2=n-m+f \leqq n -m + \frac{2}{3}m = n- \frac{1}{3}m$ . (2)　3角形を含まなければ 1 つの面は 4 本以上の辺で囲まれますので、今度は

$4f \leq 2m$ となり

$2=n-m+f \leqq n -m + \frac{1}{2}m = n- \frac{1}{2}m$ . (3)　もし全ての頂点の次数が 6 以上であれば

$2m=$ 次数の和

$\geqq 6n$ となって (1) に矛盾します。 (証明終)

※　プリントの「第3の証明」はこの Cor.19 と同じパターンを使ったものです。

辺が少ないからと言って平面的グラフとは言えない

※　Cor.19 の条件は必要条件でしかなく、

$m \leqq 3n - 6$ が成り立ったからと言って平面的であるとは言えません。 ここも大事！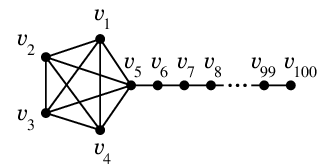

$n=100$ ,

$m=105$ なので

$m \leqq 3n -6$ は成り立つが非平面的な例 (

$K_5$ を含むので非平面的 )

前へ / 戻る / 次へ