組合せとグラフの理論(塩田)第10回 (2) 双対性
双対性
証明 (1) $G\as$ が平面グラフになることは描き方よりわかります。 $G\as$ の連結性は「 $G$ の面が順番にたどれる」ということです。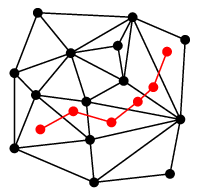
双対グラフの双対グラフは自分自身に戻ります。 証明 図では双対グラフに赤色を使って述べていきます。
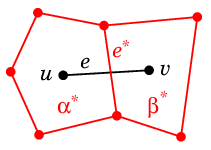
- $G\as$ の面 $\alpha\as$ の境界辺の 1 つを $e\as$、
$e\as$ がまたいでいる $G$ の辺を $e=uv$ とすると、
$u$, $v$ のどちらか一方は面 $\alpha\as$ の中にあります。
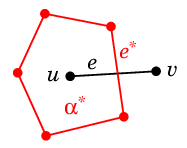
- つまり $G\as$ の各面 $\alpha\as$ には $G$ の頂点 $u$ が 1 つ以上あります。
- 2° の対応を $\varphi:\alpha\as \mapsto u$ と表すと、 $f\as=n$ ですから $\varphi$ は一対一対応であることがわかります。
- 3° の対応によって $\varphi(\alpha\as)=u$, $\varphi(\beta\as)=v$ であるとします。
このとき、
$u$ と $v$ が $G$ で隣接していること
$\Leftrightarrow$ $\ e=uv$ が $G$ の辺であること
$\Leftrightarrow$ $\ e\as$ が $\alpha\as$ と $\beta\as$ の境界であること
$\Leftrightarrow$ $\ \alpha\as$ と $\beta\as$ は $(G\as)\as$ の頂点として隣接すること