組合せとグラフの理論(塩田)第10回 (3) プラトングラフの双対性
プラトングラフの双対性
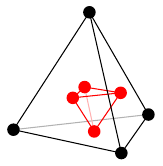
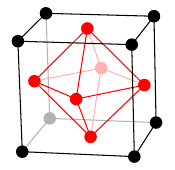
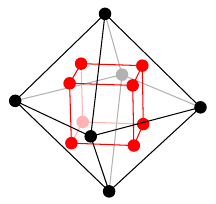
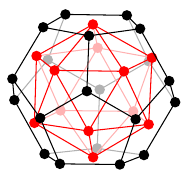
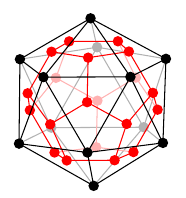
プラトングラフの双対グラフは次のように描くことができます。- 立体として考える(球面上に描くことと本質的に同じ)
- 各面の中心に点をひとつずつ打つ
- 隣り合った面に打った点同士の間に辺を描く
| $n$ | $m$ | $f$ | $n-m+f$ | |
| 正四面体グラフ | 4 | 6 | 4 | 2 |
| 立方体グラフ | 8 | 12 | 6 | 2 |
| 正八面体グラフ | 6 | 12 | 8 | 2 |
| 正十二面体グラフ | 20 | 30 | 12 | 2 |
| 正二十面体グラフ | 12 | 30 | 20 | 2 |