組合せとグラフの理論（塩田）第7回 (3)　演算 $\oplus$
前へ / 戻る / 次へ

演算 $\oplus$

　では本題に入ります。
Def.4　グラフ $G$ の辺の部分集合 $C$, $D$ に対して
$C \oplus D = C$ XOR $D$
と定める。( XOR は排他的論理和 )
$C \oplus D = (C \cup D) - (C \cap D)$
と書いても同じもので、ベン図では次の色付きの部分です。
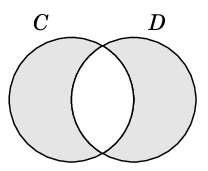
Th.5　$C$, $D$ がともに $G$ の閉路であれば、 $C \oplus D$ はいくつかの閉路を合わせたものになる。 （正確に言うと「閉路の辺集合」と言うべきですが、ルーズにしゃべります。）
証明　部分グラフとして $C \oplus D$ 上の頂点の次数は $2$ か $4$ ですので、 第5回の Th.3 より各連結成分はオイラーグラフであり、 第4回の Prop.3 よりそれは閉路に分割できます。(証明終)
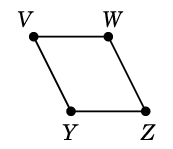
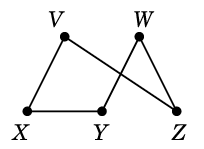
Ex.6　グラフ
$G=$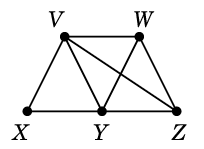
において
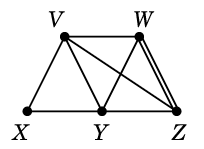
$C=$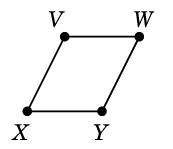 $D=$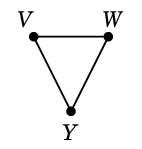
としたとき、$C \oplus D$ を求めましょう。まず $C$ と $D$ を重ねて描き、
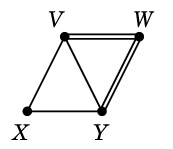
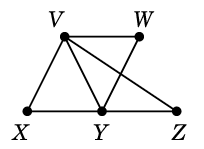
二重辺を消せば出来上がりです：
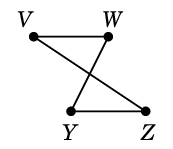
$C \oplus D=$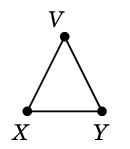
Ex.6'　 同じ $G$ において、今度は
$C=$ $D=$
とします。まず $C$ と $D$ を重ねて描き、
二重辺を消します。
$C \oplus D=$
これは次のように閉路に分割できます：
$=$ $\oplus$
次のような分け方もできます。答えは一通りとは限りません。
$=$ $\oplus$

演算 $\oplus$ の性質

Th.7（$\oplus$ の結合律）　3つの辺集合 $B$, $C$, $D$ について
$B \oplus ( C \oplus D) = (B \oplus C) \oplus D$
証明　$n$ 変数の XOR の真偽値は
  • 奇数個の変数が真 $\Rightarrow$ 真
  • 偶数個の変数が真 $\Rightarrow$ 偽
ゆえ、$\oplus$ の順番には依らない。(証明終) ... ベン図では次の色付きの部分です。

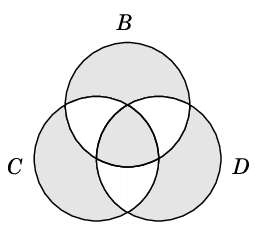※　ここから、$\require{color}\textcolor{red}{\oplus}$ を一種の「加法」だと考える ことにします。すると
Th.8（加法単位元）　空集合 $\textcolor{red}{\emptyset}$ は「ゼロ」の役割 を持つ：
$C \oplus \emptyset = \emptyset \oplus C = C$, $\quad\forall C$
Th.9（ 2倍はゼロ ）　$C \oplus C$ は「 $C$ の2倍」と考えられ、
$2 C = C \oplus C = \emptyset$, $\quad\forall C$
証明　いずれも定義より。

前へ / 戻る / 次へ