応用数学 第10回 (1) いくつかの準備
周期 $2\ell$ の場合
前回は
周期 $2\pi$ を持つ関数のフーリエ展開を扱いました。
一般に
周期 $2\ell$ を持つ関数については、変数を $\dps{\frac{\ell}{\pi}}$ 倍して定理を読みかえます。
Th.1 周期 $2\ell$ を持つ、区分的になめらかな関数 $f(x)$ はフーリエ展開
$$
f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left\{a_n\cos\left(\frac{n\pi x}{\ell}\right)+b_n\sin\left(\frac{n\pi x}{\ell}\right)\right\}
\tag{$\sharp$}
$$
を持ち、そのフーリエ係数は
$$
\left\{
\begin{array}{ll}
\dps{a_n = \frac{1}{\ell}\int_{-\ell}^{\ell}f(x)\cos\left(\frac{n\pi x}{\ell}\right)dx} & \forall n \geqq 0 \\
\dps{b_n = \frac{1}{\ell}\int_{-\ell}^{\ell}f(x)\sin\left(\frac{n\pi x}{\ell}\right)dx} & \forall n \geqq 1 \\
\end{array}
\right.
\tag{$\star$}
$$
によって定まる。
フーリエ余弦級数
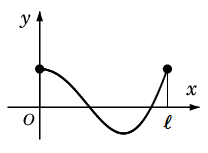
区間 $0 \leqq x \leqq \ell$ だけで定義されている関数 $f(x)$ があるとき、
区間 $-\ell \lt x \lt 0$ での値を
$\dps{f(x)=f(-x)}$
と定義し、さらにこれを周期 $2\ell$ を持つように全ての $x$ に拡張すると、周期 $2\ell$ の
偶関数 が得られます。
$\quad\longrightarrow\quad$
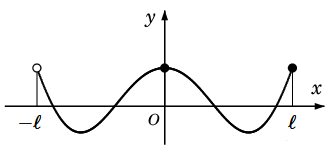
そのフーリエ展開は $\cos$ だけで表されますので
Th.2 区間 $0 \leqq x \leqq \ell$ で定義されている、区分的になめらかな関数 $f(x)$ は、フーリエ係数
$\dps{a_n = \frac{2}{\ell}\int_{0}^{\ell}f(x)\cos\left(\frac{n\pi x}{\ell}\right)dx}$ ( $n \geqq 0$ )
を用いて
$\dps{f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos\left(\frac{n\pi x}{\ell}\right)}$
( $0 \leqq x \leqq \ell$, $x$ は連続点 )
と表される。これを $f(x)$ のフーリエ余弦級数 ( フーリエ余弦展開 ) と呼ぶ。
フーリエ正弦級数
同様に区間 $-\ell \lt x \lt 0$ での値を
$\dps{f(x)=-f(-x)}$
と定義し、さらにこれを周期 $2\ell$ を持つように全ての $x$ に拡張すると、今度は周期 $2\ell$ の
奇関数 が得られます ( 不連続点以外で ) 。
$\quad\longrightarrow\quad$
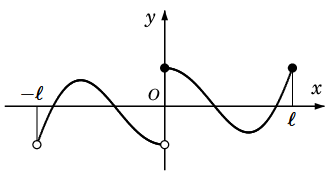
Th.2' 区間 $0 \leqq x \leqq \ell$ で定義されている、区分的になめらかな関数 $f(x)$ は、フーリエ係数
$\dps{b_n = \frac{2}{\ell}\int_{0}^{\ell}f(x)\sin\left(\frac{n\pi x}{\ell}\right)dx}$ ( $n \geqq 1$ )
を用いて
$\dps{f(x)=\sum_{n=1}^{\infty}b_n\sin\left(\frac{n\pi x}{\ell}\right)}$
( $0 \leqq x \leqq \ell$, $x$ は連続点 )
と表される。これを $f(x)$ のフーリエ正弦級数 ( フーリエ正弦展開 ) と呼ぶ。
※ 区間 $0 \leqq x \leqq \ell$ で定義されている関数を
強引に周期 $2\ell$ に拡張します ので、
$-\ell \lt x \lt 0$ での値の決め方には無限の自由度があり、
同じ関数でも $\cos$ だけで書いたり $\sin$ だけで書いたりできる、ということです。
補題
もうひとつ補題を述べます。
Lemma 3 $k$ を定数とし、2 階微分方程式
$$
\left\{
\begin{array}{l}
y''(x)+k\,y(x)=0 \quad (\ 0 \leqq x \leqq \ell\ ) \\
y(0)=y(\ell)=0 \\
\end{array}
\right.
\tag{6.11}
$$
を考える。このとき、
- $(6.11)$ が $y \equiv 0$ 以外の解を持つこと
$\Leftrightarrow$ $k \gt 0$ かつ $\exists$ 自然数 $n$
such that $\dps{\sqrt{k}=\frac{n\pi}{\ell}}$
- (1) のとき、$(6.11)$ の一般解は
$\dps{y(x)=A\sin\left(\frac{n\pi x}{\ell}\right)}$
証明 第4回 Th.2 より $y''+k\,y=0$ の一般解は
- $k \gt 0$ のとき $y=A\sin(\lambda x) + B\cos(\lambda x)$, $\lambda=\sqrt{k}$
- $k \lt 0$ のとき $y=Ae^{\lambda x} + Be^{\lambda x}$, $\lambda=\sqrt{-k}$
- $k = 0$ のとき $y=Ax+B$
です。このうち $y \not \equiv 0$ で境界条件 $y(0)=y(\ell)=0$ を満たし得るのは i の
$y=A\sin(\lambda x) + 0 \cos(\lambda x)$ かつ $\sin(\lambda\ell)=0$
のときのみで、第2式から
$\dps{\sqrt{k}=\lambda=\frac{n\pi}{\ell}}$, $\exists$ 自然数 $n$
となります。(証明終)