定数係数２階同次線形微分方程式

1. $e^{\alpha x}$ が $(8.2)$ の解であることは $$\begin{align} (e^{\alpha x})''+a\,(e^{\alpha x})'+b\,(e^{\alpha x}) &=(\alpha^2\,e^{\alpha x})+ a\,(\alpha\,e^{\alpha x})+b\,(e^{\alpha x})\\ &=(\alpha^2+a\,\alpha+b)(e^{\alpha x})=0 \\ \end{align}$$ よりわかります。$e^{\beta x}$ も同様です。 $e^{\alpha x}$ と $e^{\beta x}$ が一次独立であることは、 直接示しても簡単ですし、 前回の Ex.3, Th.4 からもわかります。
2. $\alpha$ が重根ならば $a = -2\alpha$ ゆえ $$\begin{align} (xe^{\alpha x})''&+a\,(xe^{\alpha x})'+b\,(e^{\alpha x}) \\ &=(2\alpha\,e^{\alpha x}+\alpha^2\,x\,e^{\alpha x})+a\,(e^{\alpha x}+\alpha\,x\,e^{\alpha x})+b\,(e^{\alpha x})\\ &=(2\alpha+a)(e^{\alpha x})+(\alpha^2+a\,\alpha+b)(e^{\alpha x})=0 \\ \end{align}$$ となり、$xe^{\alpha x}$ も解であることがわかり、 $e^{\alpha x}$ と $xe^{\alpha x}$ が一次独立であることも簡単に示せます。
3. (1) とは実数か複素数かが違うだけで、$e^{(\lambda+i\mu)x}$, $e^{(\lambda-i\mu)x}$ は２つの一次独立な解です。 オイラーの公式より $e^{(\lambda+i\mu)x}=e^{\lambda x}(\cos(\mu x) \pm i\, \sin(\mu x))$ ですから、$e^{\lambda x}\sin(\mu x)$, $e^{\lambda x}\cos(\mu x)$ も２つの一次独立な解になります。

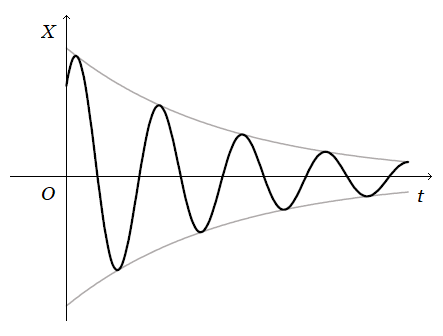
Ex.3 　前回の「鉛直ばね振り子」の微分方程式 $\dps{X''+\frac{R}{m}X'+\frac{k}{m}X=0}$ は、 特性根が共役な複素数 $\lambda\pm i\mu$ ( $\lambda \lt 0$ ) の場合で、三角関数の合成により $\dps{X(t)=C\,e^{\lambda x}\sin(\mu t + \nu)}$ と書けますから のような運動をします。