応用数学 第12回 (4) 双曲線関数
$\newcommand{\LT}{\mathscr{L}}$
双曲線関数
Def.7 次の関数を双曲正弦・双曲余弦 ( hyperbolic sine, hyperbolic cosine ) と呼ぶ：
$\dps{\sinh(t)=\frac{1}{2}(e^t-e^{-t}),\qquad
\cosh(t)=\frac{1}{2}(e^t+e^{-t})}$
その名前の由来は
Rem.8 単位円上の点が $(\cos\theta,\, \sin\theta)$ とパラメータ表示できることのアナロジーで
直角双曲線 $x^2-y^2=1$ 上の点は $(\cosh(t),\,\sinh(t))$ とパラメータ表示できる。
また
$\cosh'(t)=\sinh(t)$, $\qquad\sinh'(t)=\cosh(t)$
が成り立ち、いずれも微分方程式
$y''=y$
の解である。
また、$\cosh$ は身近なところにあるというお話で、
Rem.9 弾力の無いひもを２点で固定して吊るしたとき、
ひもが描く曲線は懸垂線と呼ばれ、
適切な座標を取れば $y=\cosh(x)$ と相似になる。
さて、双曲線関数のラプラス変換は次の通りです。
Th.10 $\dps{\LT(\cosh(\lambda t))=\frac{s}{s^2-\lambda^2}}$,
$\dps{\LT(\sinh(\lambda t))=\frac{\lambda}{s^2-\lambda^2}}$
( $s \gt |\,\lambda\,|$ ).
証明
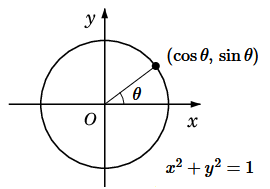
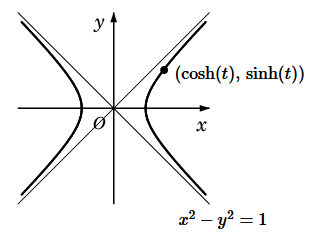
\begin{align}
\LT(\cosh(\lambda t))
&=\frac{1}{2} \int_0^{\infty} (e^{\lambda t}+e^{-\lambda t})\,e^{-st}dt \\
&=\frac{1}{2} \int_0^{\infty} \Big(e^{(\lambda-s)t}+e^{-(\lambda+s)t}\Big)\,dt \\
&=\frac{1}{2} \Bigg[ \frac{1}{\lambda-s}e^{(\lambda-s)t}-\frac{1}{\lambda+s}e^{-(\lambda+s)t}\Bigg]_0^{\infty} \\
&=\frac{1}{2} \left( -\frac{1}{\lambda-s}+\frac{1}{\lambda+s}\right) =\frac{s}{s^2-\lambda^2}, \\
\end{align}
\begin{align}
\LT(\sinh(\lambda t))
&=\frac{1}{2} \int_0^{\infty} (e^{\lambda t}-e^{-\lambda t})\,e^{-st}dt \\
&=\frac{1}{2} \int_0^{\infty} \Big(e^{(\lambda-s)t}-e^{-(\lambda+s)t}\Big)\,dt \\
&=\frac{1}{2} \Bigg[ \frac{1}{\lambda-s}e^{(\lambda-s)t}+\frac{1}{\lambda+s}e^{-(\lambda+s)t}\Bigg]_0^{\infty} \\
&=\frac{1}{2} \left( -\frac{1}{\lambda-s}-\frac{1}{\lambda+s}\right) =\frac{\lambda}{s^2-\lambda^2}. \\
\end{align}
(証明終)