応用数学 第12回 (2)　ヘヴィサイドの単位関数
前へ / 戻る / 次へ
$\newcommand{\LT}{\mathscr{L}}$

ヘヴィサイドの単位関数

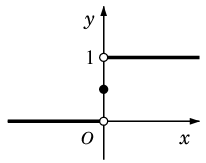
Def.3　次の階段関数をヘヴィサイドの単位関数と呼ぶ：
$\dps{ U(t)= \left\{ \begin{array}{ll} 0 & t \lt 0 \\ \frac{1}{2} & t = 0 \\ 1 & t \gt 0 \\ \end{array} \right. }\qquad\qquad$
この $U(t)$ を用いて、$\lambda \geqq 0$ に対して
$f(t)=U(t-\lambda)\qquad\qquad$
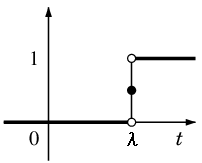
とおくと \begin{align} \LT(f)(s) & = \int_0^{\infty} U(t-\lambda) e^{-st} dt \\ & = \int_{\lambda}^{\infty} e^{-st} dt \\ & = \left[\frac{1}{-s}e^{-st}\right]_{\lambda}^{\infty} =\dps{\frac{1}{s}e^{-\lambda s}} \quad \mbox{ if }\ s \gt 0 \end{align}

前へ / 戻る / 次へ