数値解析 課題4 ( 1月11日出題 )
課題
次の課題Aまたは課題Bを解け。(両方やった場合はそれなりに加点します。)課題A
LU分解法をプログラミングし、 次式で定める $n$ 次のヒルベルト行列 $A$ と $n$ 次元ベクトル $\xxx$ に対し、 $n=4,8,16,32,64$ の場合に $A\xxx=\bbb$ の解 $\xxx$ を計算せよ。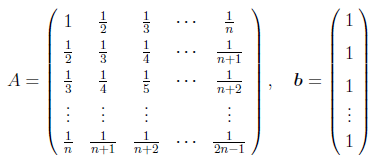
課題B
ヤコビ法とガウス・ザイデル法をプログラミングし、 次式で定める $n$ 次行列 $A$ と $n$ 次元ベクトル $\bbb$ に対し、 $n=4,8,16,32,64$ の場合に方程式 $A\xxx=\bbb$ の解 $\xxx$ を 計算し、収束までに要するステップ数を比較せよ。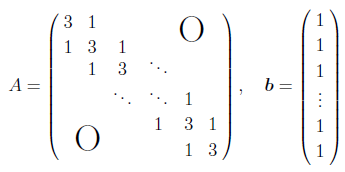
注意
- プログラムを共同製作した場合はその旨を必ず明記すること。
- 雛形プログラム
- 課題A ( utf-8 ) : LU_hinagata_utf8.c
- 課題B ( utf-8 ) : JGS_hinagata_utf8.c
- 課題A ( shift-JIS ) : LU_hinagata_shiftJIS.c
- 課題B ( shift-JIS ) : JGS_hinagata_shiftJIS.c
(右クリック → リンク先を名前を付けて保存 で保存すれば文字化けしないと思います。) - 雛形を使った場合は、プログラムリストは自作の部分のみで良い。
- 実行結果は実行出力を全て載せるのではなく、適切にまとめよ。
提出方法
- メールにて shiota@is.kochi-u.ac.jp 宛て。
- 件名は [自分の学籍番号] 数値解析課題4
- テキストでも、WORD, PDF 等のドキュメントでも可。
提出期限
- 1月25日(水) 10:20
- 原則として締め切り厳守
課題プリント ( このページとほぼ同じ内容の pdf です。)