数値解析 第8回 (2) オイラー法
オイラー法のアイデア
最初に、精度はそれほど良く無いのですが、考え方の基本となるオイラー法を紹介します。刻み幅 $h$ が小さければ、区間 $[\,x_n,x_{n+1}\,]$ 内では
オイラー法の公式
$x=x_0$ では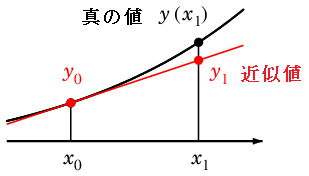
実行例
教科書 p.191 図 9.2 では刻み幅を 1/1024 まで細かくしても 0.45% ほどの誤差を生じています。数値解析 第8回 (2) オイラー法
オイラー法のアイデア
最初に、精度はそれほど良く無いのですが、考え方の基本となるオイラー法を紹介します。オイラー法の公式
$x=x_0$ では
実行例
教科書 p.191 図 9.2 では刻み幅を 1/1024 まで細かくしても 0.45% ほどの誤差を生じています。