数値解析 第6回 (3) 台形公式
台形公式
最初はシンプルに、小区間 $[\,\alpha,\beta\,]$ での積分値を台形の面積で近似します:
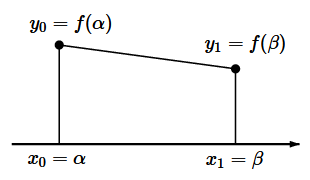
すなわち
台形公式 ( 小区間 )
$\dps{\int_{\alpha}^{\beta}f(x)dx}$ ≒ $\dps{\frac{\beta-\alpha}{2}\big(\,f(\alpha)+f(\beta)\,\big)}$
このとき、前ページの設定値は
$m=1$, $x_0=\alpha$, $x_1=\beta$,
$y_0=f(x_0)=f(\alpha)$, $y_1=f(x_1)=f(\beta)$,
$\dps{w_0=w_1=\frac{\beta-\alpha}{2}=\frac{b-a}{2N}}$
ということになります。
( 小区間は全体を $N$ 等分したものなので $\dps{\beta-\alpha=\frac{b-a}{N}}$ であることに注意してください。)
積分区間 $[\,a,b\,]$ 全体としては、
刻み幅 $\dps{\frac{b-a}{N}}$ で折れ線グラフを描いて、その面積を積分値の近似値とします。
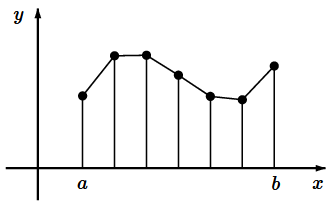
台形公式 ( 全区間 ) $\dps{h=\frac{b-a}{N}}$ として
$\dps{\int_{a}^{b}f(x)dx}$
≒ $\dps{\frac{h}{2}\left(f(a)+2\sum_{k=1}^{n-1}f(a+kh)+f(b)\right)}$



