戻る / 次へ

状況設定

　$y=f(x)$ を未知の関数とし、 その値が観測点 $x_0 \lt x_1 \lt \cdots \lt x_n$ でしかわかっていない とします。 このとき、区間 $x_0 \lt x \lt x_n$ 内の値 $x=\alpha$ における 関数値 $f(\alpha)$ を推定 しましょう。

　以下、$x_k$ での関数値 ( 観測値 ) を

$y_k=f(x_k)$   ( $k = 0,1,\cdots,n$ ) と書き、

• 入力は
  • $y=f(x)$ のグラフが通って欲しい点の座標 $(x_k, y_k)$ ( $k = 0,1,\cdots,n$ ) と
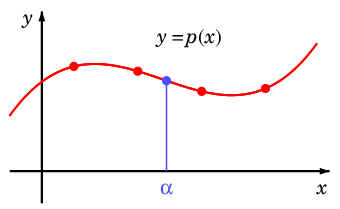
  • $\alpha$ の値
• 出力は
  • $f(\alpha)$ の推定値

というアルゴリズムを作ってゆきます。

方針

　今日紹介する方法に共通する方針は次の通りです。

1. $x=\alpha$ の付近で $f(x)$ ≒ $p(x)$ となると思われる多項式関数 $p(x)$ を作る。
2. $p(\alpha)$ を $f(\alpha)$ の推定値として出力する。

※　この $p(x)$ の作り方にいろいろな流儀がある、という訳です。 まずラグランジュ補間を説明します。

戻る / 次へ