数値解析 第3回 (3) ニュートン法
ニュートン法のアイデア
次の紹介するニュートン法 ( ニュートン・ラフソン法とも呼ぶ ) は
反復法 の典型です。
単純なループを回して解 $\alpha$ に収束する数列を作ります。
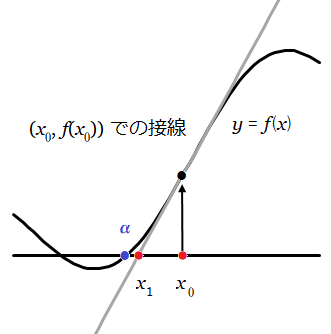
ニュートン法のアイデア $x_0$ が解 $\alpha$ に近いとき、
$y=f(x)$ のグラフの $(x_0,f(x_0))$ における接線 $\ell$ と $x$ 軸の交点を $(x_1, 0)$ とすると
$x_1$ は $x_0$ よりもっと $\alpha$ に近い値となる。
ということは、同様に $(x_1,f(x_1))$ から接線を引いて $x_2$ を、
$(x_2,f(x_2))$ から接線を引いて $x_3$ を、$\dots$ と数列を作ってゆけば
$x_n \rightarrow \alpha$ ( $n \rightarrow \infty$ )
となりそうです。
ニュートン法のアルゴリズム
式で書けば
$\ell\ :\ y-f(x_0)=f'(x_0)(x-x_0)$
ですから、$y=0$ を入れて $x_1$ を求めると
$\dps{x_1=x_0-\frac{f(x_0)}{f'(x_0)}}$
となります。これを漸化式にしたのが
Alg.7 ( ニュートン法 )
- $x_0=$ 適当な初期値, $n=0$ とする
- $\dps{x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}}$, $n=n+1$ とする
- if ( 終了条件 ) $x_n$ を出力して終了; else 2° へ戻れ;
終了条件としては次のような条件を設定します。
- $|\,f(x_n)\,|$ が十分に小さい
- $|\,x_n-x_{n-1}\,|$ が十分に小さい
ただし数列 $\{\,x_n\,\}$ の収束は保証されていないので、ループ回数にも上限を設定します。
Ex.8 $f(x)=x^2-a$ ( $\alpha=\pm\sqrt{a}$ ) のとき、ニュートン法の漸化式は
$\dps{x_{n+1}=\frac{1}{2}\left(x_n+\frac{a}{x_n}\right)}$
となります。$a=2$, $x_0=1$, 許容誤差 $=10^{-12}$ として実行すると
x0 = 1
x1 = 1.5
x2 = 1.4166666666666665
x3 = 1.4142156862745097
x4 = 1.4142135623746899
x5 = 1.414213562373095
となり、ループ5回で $\sqrt{2}$ が充分な精度で計算できました。
