数値解析 第6回 (4) ニュートン・コーツの公式
ラグランジュ補間の利用
台形公式は、$y=f(x)$ の線形補間を $y=p(x)$ として
$\dps{\int_{\alpha}^{\beta} f(x) dx}$ ≒ $\dps{\int_{\alpha}^{\beta} p(x) dx}$
と近似する公式、と言えます。
そこでもっと次数を上げて $m$ 次のラグランジュ補間 ( $m \geqq 2$ ) を用いることを考えてみましょう。
- $m$ 次のラグランジュ補間は $m+1$ 個の観測点で決めましたので、
小区間 $[\,\alpha,\beta\,]$ を更に $m$ 等分して
$\alpha = x_0 \lt x_1 \lt \cdots \lt x_m = \beta$
とします。$x_k$ は
$\dps{x_k=\alpha + k \left(\frac{\beta-\alpha}{m}\right)
=\alpha + k \left(\frac{b-a}{Nm}\right)}$ ( $k=0,1,\cdots,m$ )
と書けます。
- $\{\,(x_k,y_k)\,\}_{k=0,1,\cdots,m}$ に関する $m$ 次ラグランジュ補間多項式を $p(x)$ として
$\dps{\int_{\alpha}^{\beta} f(x) dx}$ ≒ $\dps{\int_{\alpha}^{\beta} p(x) dx}$
と近似します。
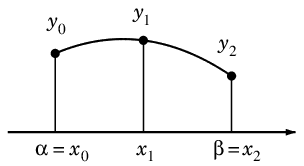
例えば 2 次のラグランジュ補間を用いるときは、
小区間 $[\,\alpha,\beta\,]$ の両端を $x_0$, $x_2$, 中点を $x_1$ として
$\{\,(x_k,y_k)\,\}_{k=0,\,1,\,2}$ を通る放物線が $y=p(x)$ になり、
ます。
ニュートン・コーツの公式
こう書いてくると $p(x)$ を具体的に求める必要があるように思えますが、
実はその必要はありません。
公式 (8.20) ( 小区間 )
$\dps{\int_{\alpha}^{\beta}f(x)dx}$
≒ $\dps{\mathit{\Delta} x \times \sum_{k=0}^{m} c_k \times y_k}$
ただし
- $\mathit{\Delta}x=$ ( $x$ の刻み幅 ) $\dps{=\frac{\beta-\alpha}{m}=\frac{b-a}{Nm}}$,
- $x_k=\alpha+k\mathit{\Delta} x $,
- $y_k=f(x_k)$
で、$c_k$
は表 ( 教科書 p.176, 表8.1 など ) から拾って使う。
※ 積分区間全体ではこの値を全ての小区間について足し合わせます。
公式 (8.20) の仕組み たとえば $m=2$ のとき、
$p(x)$ は 3 つの 2 次式 $p_0(x)$, $p_1(x)$, $p_2(x)$ を用いて
$p(x)=y_0 \times p_0(x) + y_{1} \times p_{1}(x) + y_{2} \times p_{2}(x)$
と書けていました(
第4回参照 )。
ゆえに
$\dps{\int_{\alpha}^{\beta}p(x)dx=y_0 \int_{\alpha}^{\beta}p_0(x)dx + y_{1} \int_{\alpha}^{\beta}p_{1}(x)dx + y_{2} \int_{\alpha}^{\beta} p_{2}(x)dx}$
となりますが、この $\dps{\int_{\alpha}^{\beta}p_k(x)dx}$ の値が $\mathit{\Delta}x\times$ ( 定数 $c_k$ ) になります。
もっと詳しく見る
$c_k$ の計算式は
$\dps{c_k=\int_0^m \Bigg(\ \mathop{\prod_{0 \leqq j \leqq m}}_{j \neq m} \frac{t-j}{k-j}\ \Bigg) \,dt}$
です。例えば $m=2$ のときの $c_1$ は
$\dps{c_1=\int_0^2 \left(\frac{t-0}{1-0}\right)\left(\frac{t-2}{1-2}\right) \,dt=\frac{4}{3}}$
となります。$c_k$ には次のような性質もあります:
- $c_{m-k}=c_k$ すなわち $c_k$ の表は左右対称になる
- $\dps{\sum_{k=0}^m c_k = m}$
$m=1,2,3$ のときのニュートン・コーツの公式
には別名が付いています:
$m=1$ のときは 台形公式 でした。
$m=2$ のときを シンプソンの公式 と言います:
$\dps{\int_{\alpha}^{\beta}f(x)dx}$ ≒ $\dps{\frac{\beta-\alpha}{6}(y_0+4y_1+y_2)}$
$m=3$ のときを シンプソンの $\dps{\frac{3}{8}}$ 公式 と言います:
$\dps{\int_{\alpha}^{\beta}f(x)dx}$ ≒ $\dps{\frac{\beta-\alpha}{8}(y_0+3y_1+3y_2+y_3)}$
ちょっと脱線
昔、香辛料会社の S&B から
「3/8 チップ」( = 5/8 チップの弟分 )
というポテトチップが販売されていました。
ネイミングを考えた人は理系の大学を出た人に違いないと思ったものです。
実装上の注意
次数 $m$ を大きくするとラグランジュ補間には不自然な凹凸ができ(ルンゲ現象)、
積分値の精度にも影響が出てくるので、
$m$ を大きくするよりは、
積分区間の分割数 $N$ を大きくする方が良いとされています。
