数値解析 第4回 (2) ラグランジュ補間
線形補間 ( = 1 次のラグランジュ補間 )
言葉はいかめしいですが、折れ線グラフのことです。
「線形」とは「 1 次式」のことですから、線分でつなぐ、という意味です。
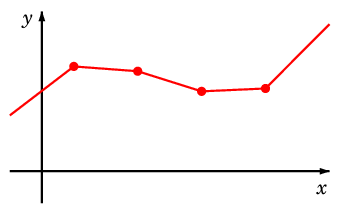
グラフが通って欲しい点 $(x_k, y_k)$ ( $k = 0,1,\cdots,n$ ) を順に線分でつなぐだけですから、
見るからに滑らかさに欠けています。
2 次のラグランジュ補間
2 次関数を使うと丸みも表現できるのではないか、と考えて次のアルゴリズムを考えます。
Alg.1 ( 2 次のラグランジュ補間 )
- $x_k \lt \alpha \lt x_{k+2}$ となる番号 $k$ を選ぶ。
- 2 次式 $p(x)$ を
$p(x_i) = y_i$ ( $i=k$, $k+1$, $k+2$ )
となるように作る。
- $p(\alpha)$ を出力する。
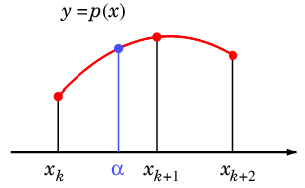
その $p(x)$ はどうやって作るのでしょうか。
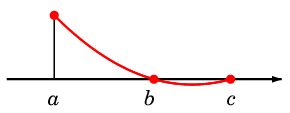
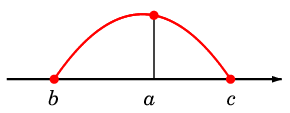
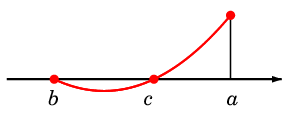
Lemma 2
$\left\{
\begin{array}{ll}
x = a &\!\!\mbox{で } 1 \\
x = b, \,c &\!\!\mbox{で } 0 \\
\end{array}
\right.$
となる 2 次式は何か?
答え
$x = b,\, c$ で $0$ となる 2 次式としては
$(x-b)(x-c)$
がすぐ思いつきます。
$x = a$ での値を $1$ にしたければ定数倍で調整すれば良く、答えは
$\dps{\frac{(x-b)(x-c)}{(a-b)(a-c)}}$
です。
Alg.3 ( $p(x)$ の作り方 )
- Lemma 2 を用いて 3 つの 2 次式 $p_0$, $p_{1}$, $p_{2}$ を次のように作る:
| $p_0$ | $p_{1}$ | $p_{2}$ |
| $x=x_k$ での値 | 1 | 0 | 0 |
| $x=x_{k+1}$ での値 | 0 | 1 | 0 |
| $x=x_{k+2}$ での値 | 0 | 0 | 1 |
- $p(x)=y_k \times p_0(x) + y_{k+1} \times p_{1}(x) + y_{k+2} \times p_{2}(x)$ とおく。
証明 2 次式の和なので $p(x)$ は 2 次式であって、$x_k$ での値は
\begin{align}
p(x_k)
&=y_k \times p_0(x_k) + y_{k+1} \times p_{1}(x_{k+1}) + y_{k+2} \times p_{2}(x_{k+2}) \\
&=y_k \times 1 + y_{k+1} \times 0 + y_{k+2} \times 0 = y_k \\
\end{align}
同様に、
$p(x_{k+1}) = y_k \times 0 + y_{k+1} \times 1 + y_{k+2} \times 0 = y_{k+1},$
$p(x_{k+2}) = y_k \times 0 + y_{k+1} \times 0 + y_{k+2} \times 1 = y_{k+2}\,$
(証明終)
やってみよう
$p(1) = 5$,
$p(2) = 4$,
$p(3) = 6$
となる 2 次式 $p(x)$ は何か?
答え
\begin{align}
p(x)
&= \dps{5 \times \frac{(x-2)(x-3)}{(1-2)(1-3)} + 4 \times \frac{(x-1)(x-3)}{(2-1)(2-3)} + 6 \times \frac{(x-1)(x-2)}{(3-1)(3-2)} } \\
&= \dps{\frac{3}{2}x^2 - \frac{11}{2}x + 9} \\
\end{align}
$m$ 次のラグランジュ補間 ( $m \geqq 3$ )
近似多項式の次数 $m$ をどんどん上げていきましょう。
Alg.4 ( $m$ 次のラグランジュ補間 )
- $x_k \lt \alpha \lt x_{k+m}$ となる番号 $k$ を選ぶ。
- $m$ 次式 $p(x)$ を
$p(x_i) = y_i$ ( $i=k$, $k+1$, $\cdots$ $k+m$ )
となるように作る。
- $p(\alpha)$ を出力する。
たとえば 3 次であれば
$\dps{\frac{(x-b)(x-c)(x-d)}{(a-b)(a-c)(a-d)}}$
のような形で
| $p_0$ | $p_{1}$ | $p_{2}$ | $p_{3}$ |
| $x=x_k$ での値 | 1 | 0 | 0 | 0 |
| $x=x_{k+1}$ での値 | 0 | 1 | 0 | 0 |
| $x=x_{k+2}$ での値 | 0 | 0 | 1 | 0 |
| $x=x_{k+3}$ での値 | 0 | 0 | 0 | 1 |
を満たす 3 次式 $p_0$, $p_{1}$, $p_{2}$, $p_{3}$ を作って
$p(x)=y_k \times p_0(x) + y_{k+1} \times p_{1}(x) + y_{k+2} \times p_{2}(x) + y_{k+3} \times p_{3}(x)$
とおきます。4 次以上も「推して知るべし」です。
※ $m$ 次式には $m+1$ 個の係数がありますので $m+1$ 個の観測点の値を指定すると $p(x)$ は唯一つに決まります。
例
$x =0, 1, 2, 3, 4, 5, 6$ を観測点とする、1 次, 2 次, 6 次のラグランジュ補間を比較します。
( 2 次のラグランジュ補間は $[0,\,2]$, $[2,\,4]$, $[4,\,6]$ の
3 区間ごとに
Alg.1 を適用しています。)
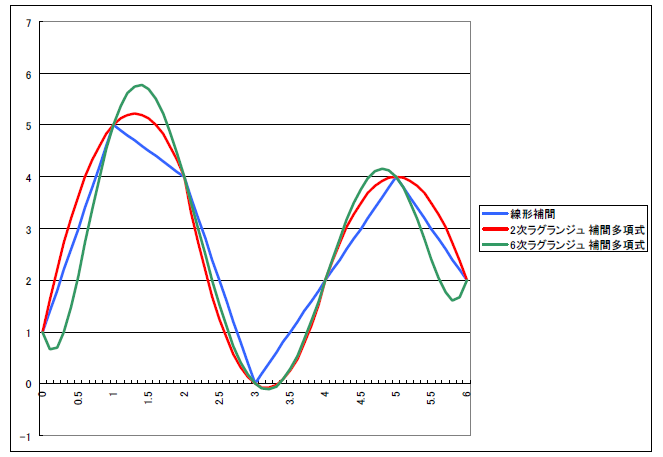
2 次はそこそこ上手くつながっていますが、
6 次は端の方で不自然に下がっているのが気になります。
次の例は 2 次も 6 次も上手く描けていません。
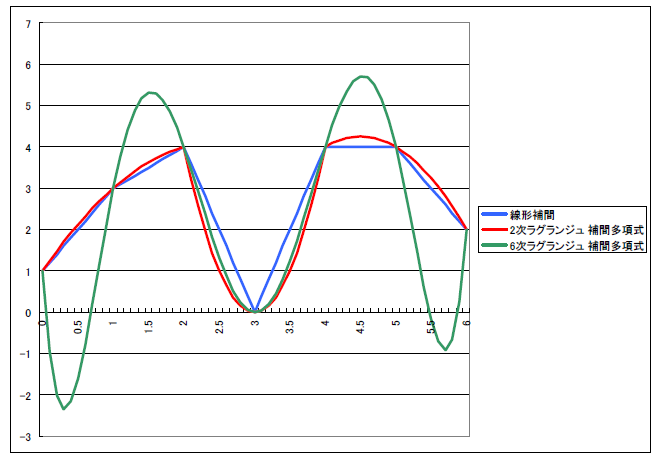
使い物にならない、と思うのは早計です。
観測点の間隔が大き過ぎるのがいけないので、
数値積分に応用するときはもっと観測点の間隔を小さくして、
精度を良くします。
観測点 $x=0$, $1$, $\cdots$, $6$ に対して観測値を指定して
1, 2, 6 次のラグランジュ補間で曲線を描く Excel ドキュメントを次の場所に置いておきます:
黄色のセルの値を書き換えると自動的にグラフも書き換えますので遊んでみてください。






