数値解析 第8回 (1) 状況設定
状況設定
- $x$ : 変数
- $y=y(x)$ : $x$ の未知関数
- $f(x,y)$ : $x$ と $y$ の 2 変数関数 ( プログラミング言語のライブラリで計算できるもの )
とするとき、次の形の微分方程式の数値解を求めます :
$$
y'(x) = f(x, y(x)),\qquad
y(x_0) = y_0
\tag{9.7}
$$
( $f$ の式と、$x_0$ と $y_0$ の値が与えられます。)
Ex.1 第2回のパラシュートの例 は ( $x$ と $y$ で書くと )
$y''=-g-Ky'$
でした。1 回積分すると
$y'=-gx-Ky+c$
となり、 $(9.7)$ で $f(x,y)=-gx-Ky+c$ の場合になります。
基本方針
例によっていろいろな手法がありますが、今日紹介する方法に共通する方針は次のとおりです:
- $x$ の刻み幅 $h$ を設定する。
- 初期条件を決める $x_0$ から $h$ 刻みで
$x_n = x_0 + n \times h$ ( $n=1,2,\cdots$ )
とおく。
- 真の値 $y(x_n)$ の近似値を $\require{color}\textcolor{red}{y_n}$ ( $n=1,2,\cdots$ ) と書くことにする。
- 順番に、
- $y_0$ の値から $y_1$ を推定し、
- $y_1$ の値から $y_2$ を推定し、
$\vdots$
- $y_n$ の値から $y_{n+1}$ を推定してゆく
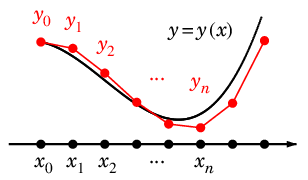
近似式の作り方(積分進行法)
$(9.7)$ より
$\dps{\int_{x_n}^{x_{n+1}}f(x,y(x))dx = \int_{x_n}^{x_{n+1}}y'(x)dx = y(x_{n+1}) - y(x_n)}$
ゆえ、真の値 $y(x_n)$ たちは
$$
\require{color}
y(x_{n+1}) = y(x_n) + \int_{x_n}^{x_{n+1}}f(x,\textcolor{red}{y(x)})dx
\tag{9.9}
$$
を満たします。
ただし $y(x)$ が未知なので、何らかの理屈をつけて右辺の積分を近似します。