アルゴリズム論特論(塩田) 2019年度教材
- 今年度は公開鍵暗号系について、その設計とアルゴリズム・計算量の講義をする予定です。
第1回 四則演算の計算量 (4.15)
- 授業内容
- 慣用記号
- 自然数 n のビット長 = O(log n)
- 2進数の計算問題 exercise01.pdf をやってみよう。
- Wikipedia で 加算器の構造 を見てみよう。
- 四則演算の計算時間を計測する Python プログラム operations.py
- ツボ
- y = log x のグラフの真の姿
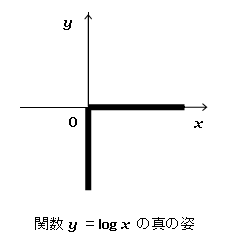
- log の関数値は極めて小さい
- n 以下の2つの正整数の四則演算の計算量は
- 加法, 減法: O(log n)
- 乗法, 除法: O(log2n)
- y = log x のグラフの真の姿
第2回 最大公約数 (4.22)
- 授業内容
- てんびんクイズ
- 問:十分大きな天秤と、a グラムと b グラムの分銅がたくさんあるとき、測ることのできる最小の重さはいくらか?
- 予想:a と b の最大公約数
- 最大公約数 gcd, 最小公倍数 lcm
- a, b の任意の公倍数は lcm(a, b) の倍数
- a, b の任意の公約数は gcd(a, b) の約数
- gcd, lcm は「単なる大小関係」で定義したのに整除関係を導く
- てんびんクイズ
- ツボ
- 2つの自然数 a, b に対して次の2つの集合は一致する:
- a x + b y ( x, y は整数 ) の形で書ける整数全体の集合
- gcd(a, b) の倍数全体の集合
- 特に、a, b を与えたとき、gcd(a, b) = a x + b y を満たす x, y が必ず存在する。
- 2つの自然数 a, b に対して次の2つの集合は一致する:
第3回 ユークリッドのアルゴリズム (5.9)
- 授業内容
- 素因数分解がわかっているときの gcd, lcm
- ユークリッドのアルゴリズム
- gcd のみ求めるアルゴリズム
- gcd(a, b) = a x + b y を満たす x, y も求めるアルゴリズム
- ツボ
- RSA暗号の計算には gcd や上記の x が必要。
- RSA暗号は素因数分解の困難さに基づくので、gcd を素因数分解で求めるのはナンセンス。
- そこでユークリッドのアルゴリズムが必要になる。
第4回 ユークリッドのアルゴリズムの計算量・再帰 ver. (5.13)
第5回 法演算、フェルマの小定理 (5.20)
- 授業内容
- 合同式
- 法演算
- 九去法
- フェルマの小定理
- ツボ
- 加法・減法・乗法・べき乗に関して、合同式はイコール感覚で使える
第6回 法 n での除算 (5.27)
- 授業内容
- 割り算と除算の違い
- mod n での逆数
- 配布プリント
- ツボ
- mod n で 1/a が存在 ⇔ gcd(a, n) = 1
第7回 剰余類、オイラーの定理、べき乗による変換 (6.3)
- 授業内容
- 剰余類、既約剰余類
- オイラー関数 φ(n) = ( 法 n の既約剰余類の個数 )
- オイラーの定理 gcd(a, n) = 1 ⇒ 法 n で a φ(n) = 1
- 定理
p が素数で、e, d が ed ≡ 1 ( mod (p-1) ) を満たす自然数ならば、
任意の整数 x に対して xed ≡ x ( mod p )
- 宿題
- 次の暗号は公開鍵暗号になり得るか?
- 平文集合 P = {0, 1, ..., p-1}
- 暗号文集合 C = {0, 1, ..., p-1}
- 暗号化関数 E(x) = xe % p
- 復号関数 D(y) = yd % p
- 次の暗号は公開鍵暗号になり得るか?
- ツボ
- フェルマの小定理は、オイラーの定理で n が素数の場合
- オイラーの定理は群論的に証明される
第8回 RSA 暗号の設計、高速べき乗法 (6.10)
- 宿題の答え
- 答えは否。暗号化に必要な暗号化指数 e と法 p は公開しなければならないが、 e と p-1 を拡張ユークリッドアルゴリズムに入力することによって復号化指数 d が高速に求められるので。
- 授業内容
- 定理 p, q を異なる2つの素数、m を p-1 と q-1 の公倍数、e, d を ed ≡ 1 ( mod m ) を満たす自然数とすると、 任意の整数 x に対して xed ≡ x ( mod p×q )
- RSA暗号 上述の定理の状況下、n = p×q と置いて、
- 平文集合 P = {0, 1, ..., n-1}
- 暗号文集合 C = {0, 1, ..., n-1}
- 暗号化関数 E(x) = xe % n
- 復号関数 D(y) = yd % n
- 高速べき乗法(反復2乗法)
- ツボ
- RSA暗号の解読は、素因数分解と同程度に困難である。
- 暗号設計に必須な xe % n の計算は、2乗を巧みに使って高速化できる。
第9回 素数生成 (6.17)
- 授業内容
- 擬素数
- フェルマ・テストによる素数判定
- 素数定理
- カーマイケル数
- ツボ
- 素数判定・素数生成も、高速べき乗法の応用で実装できる。
- フェルマ・テストによる素数生成の計算量は O(log4n)
- 宿題
- RSA暗号の鍵 p, q, n, e, d を、p が 510ビット、q が 520ビット程度になるように生成し、 公開鍵 n, e を塩田に送信せよ。秘密鍵は各自保管しておくこと。
- 折り返し塩田から暗号文を返送するので復号せよ。 正しく復号できれば復号文は8桁の数字になり、西暦4桁+月2桁+日2桁である著名人の誕生日を表している。 その著名人を答えよ。
第10回 RSA暗号に使ってはいけない危険な鍵 (6.24)
- 授業内容
- RSA暗号に使ってはいけない危険な鍵
- p, q が近いもの(フェルマ法, H28年度、田中の卒業論文)
- p と, q の簡単な有理数倍が近いもの(拡張フェルマ法, H29年度、池内の卒業論文)
- p-1 が小さな素因数しか持たないもの(p-1法)
- p+1 が小さな素因数しか持たないもの(p+1法, H27年度、寺本の卒業論文)
- 有名な素数を用いたもの etc.
- サンプルプログラム
- 暗号ライブラリ crypto.py
- フェルマ法 FermatMethod.py
- 拡張フェルマ法1 ModifiedFermatMethod_odd.py
- 拡張フェルマ法2 ModifiedFermatMethod_even.py
- p-1 法 p-1Method.py
- p+1 法 p+1Method.py
- RSA暗号に使ってはいけない危険な鍵
- ツボ
- RSA暗号と言えども、不用意に鍵を作ると危ない。
第11回 mod p の乗法構造 (7.1)
- 授業内容
- 元の生成する部分群
- 元の位数
- mod p の原始根
- 離散対数問題
- 配布プリント
第12回 Diffie-Hellman 鍵交換システム (7.8)
参考資料
- 計算機システムでの Python
- Windows へのインストール方法(「情報処理」教材)
- Windowsユーザの為の環境整備
- Tera Pad のツール設定例
- 平成9年度教材 (暗号アルゴリズム、pdfファイル)
サンプルプログラムについて
- Python のサンプルプログラムは IDLE または cygwin のコマンドラインで実行することを想定して書いてありますので、 各自の環境に合わせて適宜変更を加えてください。
- 1行目の #!/usr/bin/env python はコマンドラインで実行するためのおまじない
- 2行目の #-*- coding: utf-8 -*- は日本語コード指定
- ダブルクリックで起動させて使いたい人は、プログラムの最後に
fin = stdin.readline()
という行を付け加えてください。 Enter キーを押すまでウィンドウが閉じなくなります。