アルゴリズム論特論（塩田）　2017年度教材　第5回

  • 復習
    • 自然数 n のビット長は O(log n)
    • n 以下の２数の加法の計算量は O(log n)
    • n 以下の２数の減法の計算量は O(log n)
    • n 以下の２数の乗法の計算量は O(log2n)
    • a ÷ b の計算量は、商を q として O(log b× log q)
    • n 以下の２数の除法の計算量は大雑把に O(log2n)
    • ユークリッドのアルゴリズムは、入力 a, b に対して、gcd(a, b) と、gcd(a, b)= ax + by を満たす x, y が出力される
    • ユークリッドのアルゴリズムの入力を a, b ( a > b > 0 ) とするとき、その計算量は O(log2a)

  • 授業内容
    • 合同式の定義
    • 法演算
    • 九去法

  • ツボ
    • 加法・減法・乗法・べき乗に関して、合同式はイコール感覚で使える

  • 宿題
    1. 二項係数（組合せの数）、順列の数は何を数えているのか
    2. 二項係数が 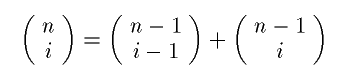を満たすのは何故か

戻る