2次曲面の分類

• 3次元空間の中の2次曲面は次の6種類に分類されます：
  
  

  双曲放物面 z = x2－y2		楕円放物面 z = x2 + y2		楕円面 x2 + y2 + z2 = 4
  円錐面 z2 = x2 + y2		一葉双曲面 z2 = x2 + y2－1		二葉双曲面 z2 = x2 + y2 + 1


（座標を変換すればこのうちのどれかになります。線形代数でそのうちやるかも。）

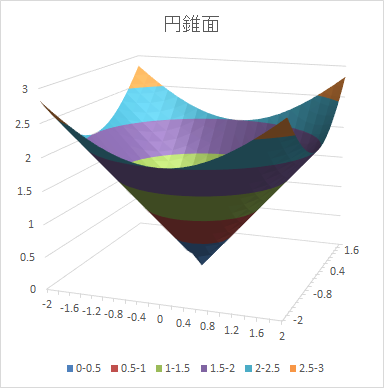
円錐面の描き方 ( L10.xlsx の円錐面のシート )

1. まず、連続データの作成で
   • A2 から A22 までのセルに -2, -1.8, ... , 2 を、
   • B1 から V1 までのセルに -2, -1.8, ... , 2 を、
   入力します。
2. B2 のセルを選択
3. 入力窓に = sqrt($a2^2 + b$1^2) と入力し Enter（ ^2 は 2乗のこと。絶対参照を使うと B2 の座標は ($a2, b$1) になるのでこの計算式が z = sqrt(x² + y²) を表します。）
4. B2 のセルを選択 → 右クリック → コピー
5. 名前ボックスに b2:v22 と入力し Enter → 貼り付け
6. A1:V22 を選択 → 挿入タブ → グラフのどれか → 等高線

発展課題

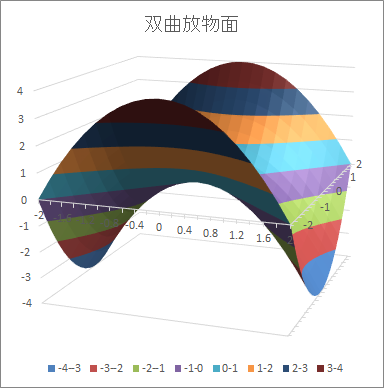
• 上の描き方をまねて双曲放物面を描いてみましょう。
  • 円錐面のシートをコピーして作り直しても構いませんが、できれば自分で一から作ってみましょう。
  • B2 に書き込む式は = $a2^2 - b$1^2 となります。


• 時間が余っている人はさらに他の曲面も描いてみましょう（B2 に書き込む式を示しておきます)。
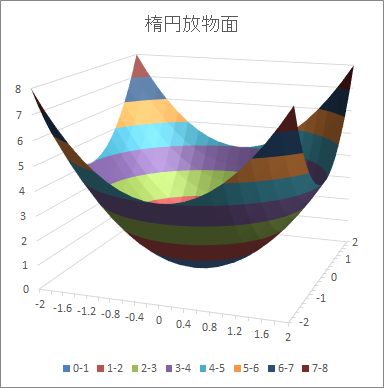
  • 楕円放物面 : = $a2^2 + b$1^2
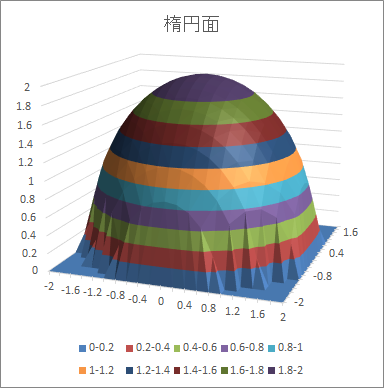
  • 楕円面 : = sqrt(4 - $a2^2 - b$1^2)
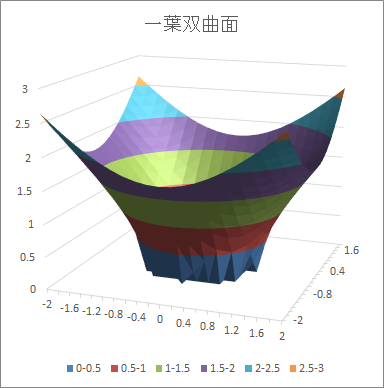
  • 一葉双曲面 : = sqrt($a2^2 + b$1^2 - 1)
  • 二葉双曲面 : = sqrt($a2^2 + b$1^2 + 1)
  
  
• 完成したら メール に添付して塩田まで提出してください。
• 宛先は shiota＠is.kochi-u.ac.jp ( ＠ は半角に直してください )
• 件名は、自分の学籍番号を入れて
  B203Q999Q　7月1日の発展課題
  のように書いてください。

まだ時間が余っている人は

• 面白い曲面を探してみましょう。

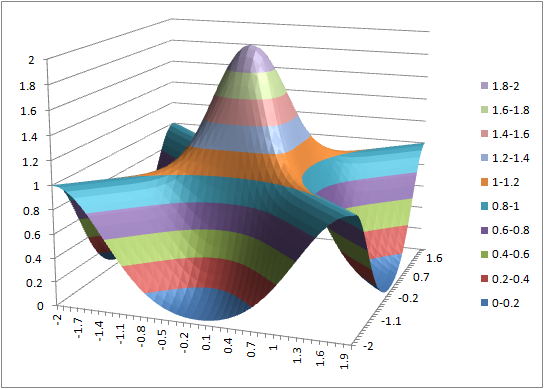
  (1)  = exp(-($a2^2+b$1^2)*2)

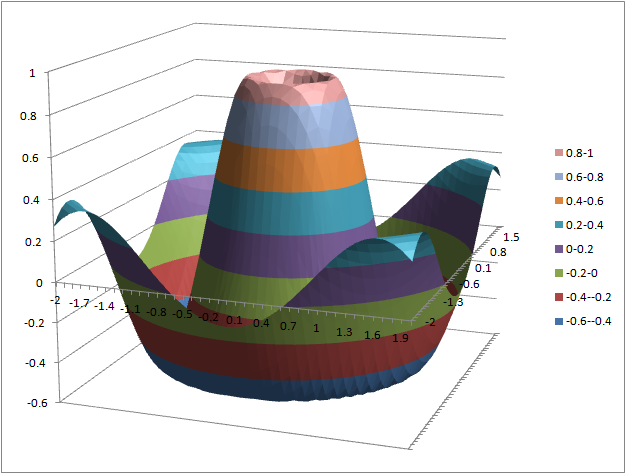
  (2)  = sin(3*sqrt($a2^2+b$1^2))/sqrt(1+$a2^2+b$1^2)

  (3)  = exp(-(abs($a2)+abs(b$1)))

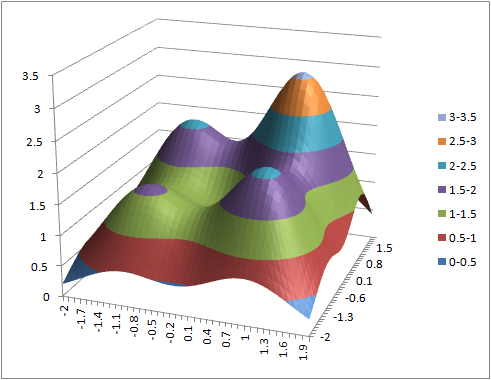
  (4)  = 1.5*exp(-(($a2+1)^2+(b$1+1)^2))+2*exp(-(($a2+1)^2+(b$1-1)^2))
            +2*exp(-(($a2-1)^2+(b$1+1)^2))+3*exp(-(($a2-1)^2+(b$1-1)^2))

  (5)  = exp(-(($a2-b$1)^2))+exp(-(($a2+b$1)^2))

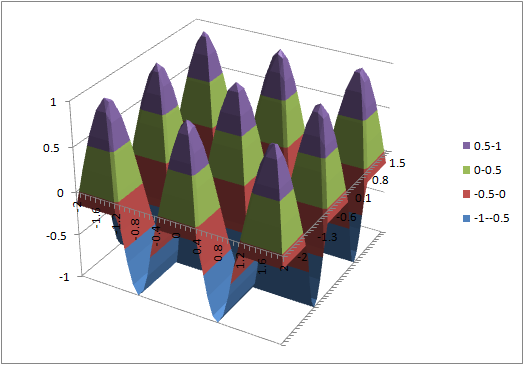
  (6)  = min(cos(4*$a2),cos(4*b$1))

  という式（セル B2 の場合）だと次のような絵が描けます:
  
  

  (1)		(2)		(3)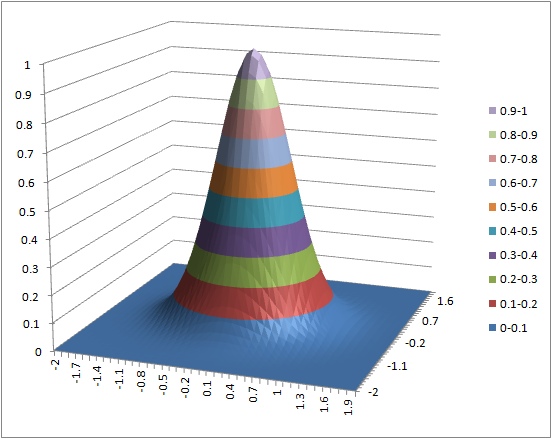
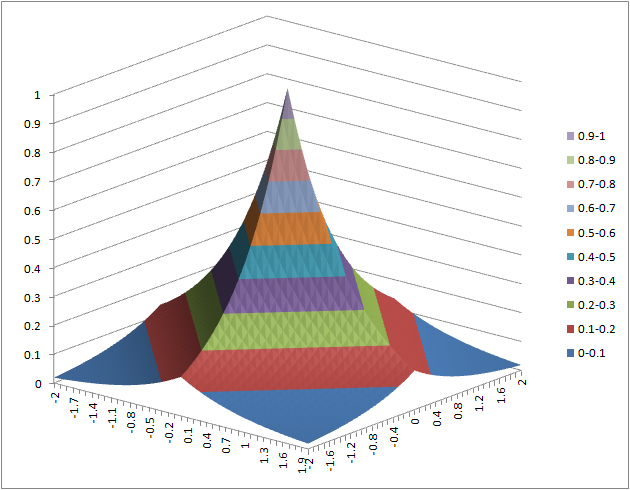
  (4)		(5)		(6)