2次曲面の分類

• 3次元空間の中の1次曲面（1次式で書ける曲面）は平面しかありません。


• 次数を1増やすと、3次元空間の中の2次曲面は次の6種類に分類されます：
  
  

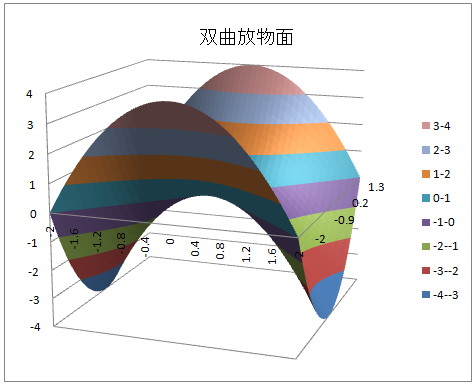
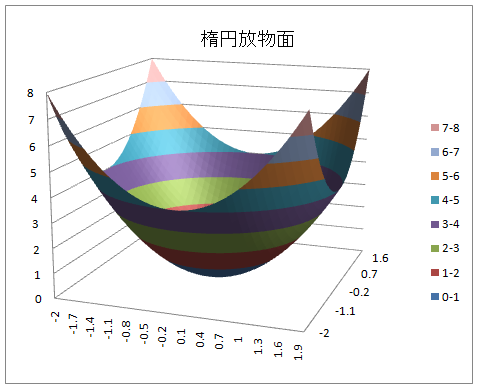
  双曲放物面 z = x2－y2		楕円放物面 z = x2 + y2		楕円面 x2 + y2 + z2 = 4
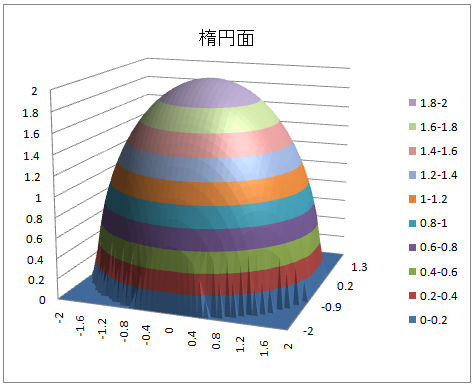
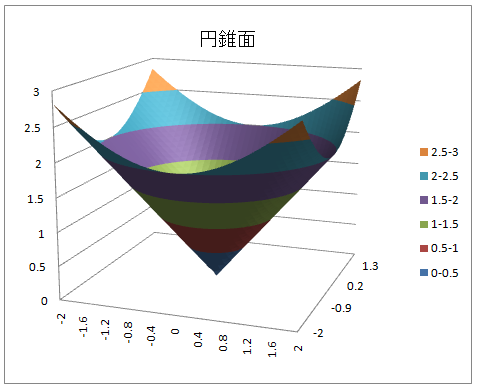
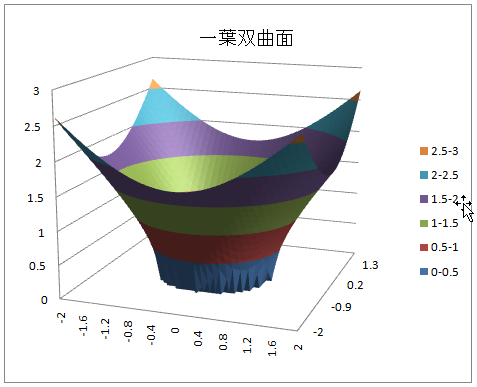
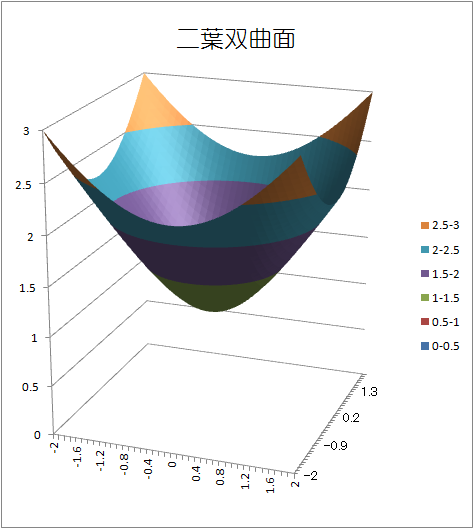
  円錐面 z2 = x2 + y2		一葉双曲面 z2 = x2 + y2－1		二葉双曲面 z2 = x2 + y2 + 1


（座標を変換すればこのうちのどれかになります。線形代数でそのうちやるかも。）

双曲放物面を描いてみよう

1. ここから雛形ファイル L09.xlsx をダウンロード。


2. まず、連続データの作成で
   • B1 から AP1 までのセルに -2, -1.9, ... , 2 を、
   • A2 から A42 までのセルに -2, -1.9, ... , 2 を
   入力します。（それぞれ x 座標、y 座標になります。）
   1. B1 のセルに -2 を入力
   2. 名前ボックスに b1:ap1 と入力し Enter
   3. ホームタグ → → 連続データの作成
   4. 増分値を 0.1 にして OK
   5. A2:A42 でも同様
   
   
3. B2 のセルを選択


4. 入力窓に = b$1^2 - $a2^2 と入力し Enter（ ^2 は 2乗のこと。絶対参照を使うと B2 の座標は (b$1, $a2) になるのでこの計算式が z = x² - y² を表す。）


5. B2 のセルを選択 → 右クリック → コピー


6. 名前ボックスに b2:ap42 と入力し Enter → 貼り付け


7. 表全体を選択 → 挿入タブ → その他のグラフ → 等高線


8. 完成したら一旦上書き保存しましょう。

課題

• 他の5種類の2次曲面もそれぞれ別のシートに描いてください。
  • 双曲放物面のシートをコピーして、
    • B2 のセルの計算式の書き換え
    • 計算式の貼り付け直し
    • グラフの作り直し
    でできるはずです。


• 式を z = で書き直すと
  • 楕円放物面 : z = x² + y²
  • 楕円面 : z = sqrt(4 - x² - y²)
  • 円錐面 : z = sqrt(x² + y²)
  • 一葉双曲面 : z = sqrt(x² + y² - 1)
  • 二葉双曲面 : z = sqrt(x² + y² + 1)


• 時間が余っている人は自由に他の曲面も描いてみましょう。

  (1)  = exp(-($a2^2+b$1^2)*2)

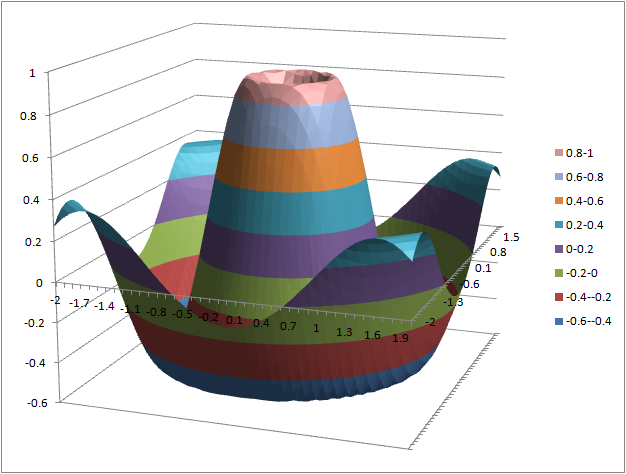
  (2)  = sin(3*sqrt($a2^2+b$1^2))/sqrt(1+$a2^2+b$1^2)

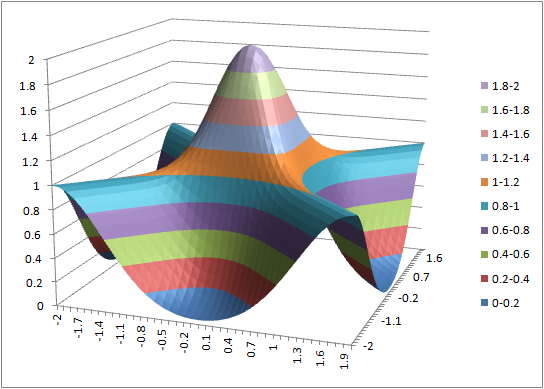
  (3)  = exp(-(abs($a2)+abs(b$1)))

  (4)  = 1.5*exp(-(($a2+1)^2+(b$1+1)^2))+2*exp(-(($a2+1)^2+(b$1-1)^2))
            +2*exp(-(($a2-1)^2+(b$1+1)^2))+3*exp(-(($a2-1)^2+(b$1-1)^2))

  (5)  = exp(-(($a2-b$1)^2))+exp(-(($a2+b$1)^2))

  (6)  = min(cos(4*$a2),cos(4*b$1))

  という式（セル B2 の場合）だと次のような式が描けます:
  
  

  (1)	(2)	(3)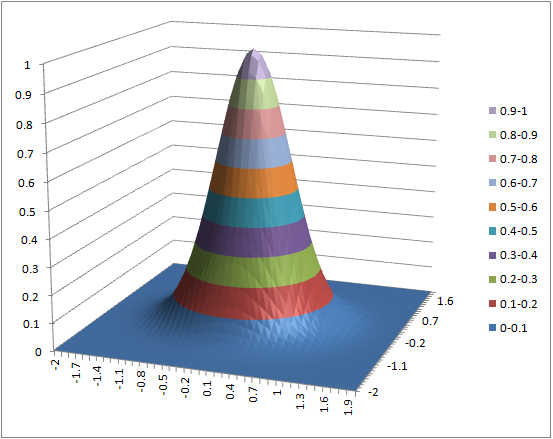
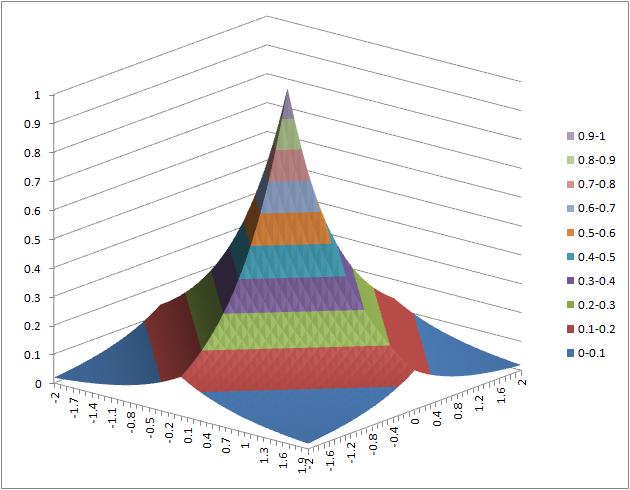
  (4)	(5)	(6)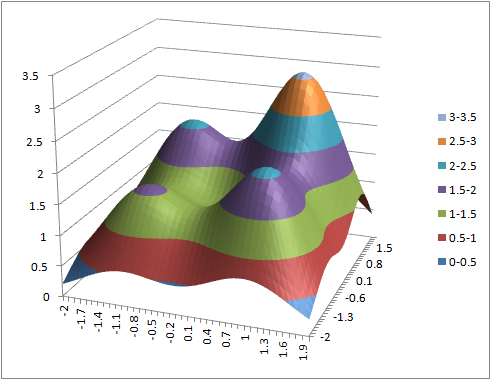



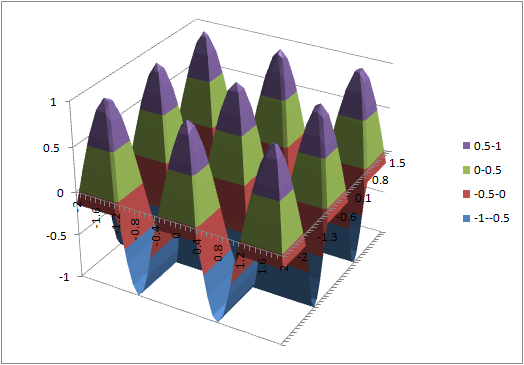
• 完成したら メール に添付して塩田まで提出してください。


• 宛先は shiota@is.kochi-u.ac.jp
• 件名に
  自分のユーザID　6月14日の課題
  と書いてください。