組合せとグラフの理論(塩田)第12回 (5) $a^{-1}$ を考える理由
$a^{-1}$ を考える理由
次のネットワークにおいて
$N$ : 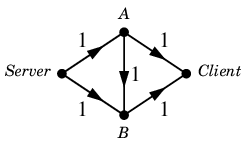
初めにこのようなフロー $\varphi$ を見つけたとしましょう。
$\varphi$ : 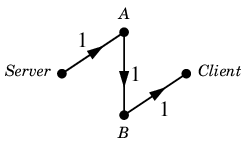
このとき $a^{-1}$ を考えずに $N'$ を作ってしまうと
失敗 $N'$ : 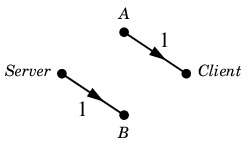
となって $N'$ には $v$-$w$ 道が無いので増加道が作れません。
ところが $a^{-1}$ を考えて $N'$ を作れば
本当の $N'$ : 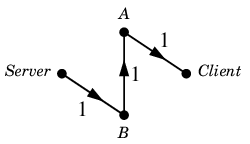
となり、次のように増加道 $\varepsilon$ が見つかります。
$\varepsilon$ : 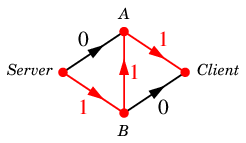
新 $\varphi=\varphi+\varepsilon$ は
新 $\varphi$ : 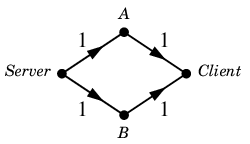
となって最大フローになります。
最初の $\varphi$ では真ん中の回線を使っていましたが、
使わなかった方が通信容量が増えた訳で
「使ってみたけどやめた」
というときのために $a^{-1}$ を登録してあるのです。
無向グラフの場合
無向グラフはどの辺も双方向に通信可能なネットワークと考えられ、
最大フローアルゴリズムを実行することができます(ただし入口・出口が自動的には決まりませんが)。
例えば完全グラフ(全ての辺の容量1)では次のような最大フローが得られます。
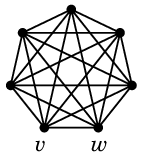 →
→ 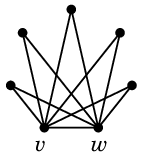
頂点数を増やすとこんな絵が描けます。

真面目なことをやってるのに奇麗な絵が描ける、という例でした。






 →
→ 
