組合せとグラフの理論(塩田)第12回 (4) 最大フローアルゴリズム実行例
最大フローアルゴリズム実行例
Ex.5 のネットワーク
$N$ : 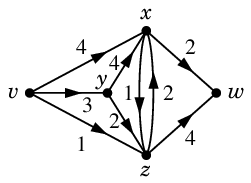
の最大フローを
Alg.12 に従って求めてみましょう。
まず適当に(容量・入出次数に気を付けて)次のフロー $\varphi$ を見つけておきます。
$\varphi$ : 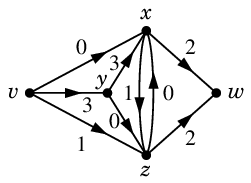 Def.9
Def.9 に従って $N'$ を作ります。
(簡単のため容量 $0$ の弧は省略してあります。)
この作業が一番煩雑なので丁寧に見てください。
$N'$ : 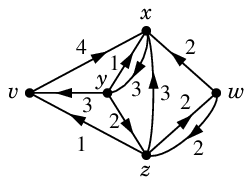
$N'$ の中で弧の向きに沿った幅優先探索を実行すると、次の赤い $v$-$w$ 道 $P$ が見つかります。
$P$ : 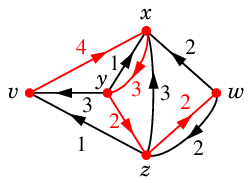
$P$ 上の弧の「残りの容量」の最小値は $2$ なので、
Def.10 の増加道 $\varepsilon$ は
次のようになります。
$\varepsilon$ : 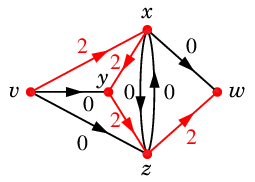
$\varphi$ と $\varepsilon$ の重みを足し合わせて新しい $\varphi$ とします。
($yx$ と $xy$ は逆向きなので、重み $3$ と $2$ を相殺して $yx$ の重みを $1$ にします。)
$\varphi$ :  $\varepsilon$ :
$\varepsilon$ : 
$\downarrow$
新 $\varphi = \varphi + \varepsilon$ : 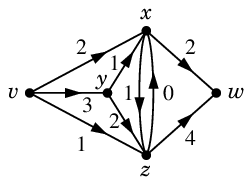 Def.9
Def.9 に戻って $N'$ を更新します。
$N'$ : 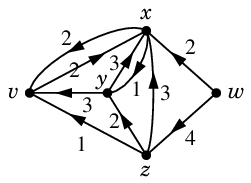
$N'$ には $v$-$w$ 道が無くなりましたので $\varphi$ が最大フローになりました。
Rem.13 弧の容量が全て整数値の場合(実用ではたいていそうです)、
Alg.12 のループ回数は多くとも容量の最大値以下ですから、
$P$ をみつけるのに幅優先探索を使えばこのアルゴリズムは高速に実行できます。





 $\varepsilon$ :
$\varepsilon$ : 







 $\varepsilon$ :
$\varepsilon$ : 

