組合せとグラフの理論(塩田)第9回 (2) クラトフスキーの定理
部分グラフの平面性との関係
平面性の判定条件については、クラトフスキーの定理、という有名な定理があります。
まずは簡単な命題から。
Prop.8 $H$ をグラフ $G$ の部分グラフとする。このとき
- が平面的 $\Rightarrow$ も平面的。
- が非平面的 $\Rightarrow$ も非平面的。
には $G$ と $H$ のどちらが入るでしょうか。
答えは自分で考えてから
Prop.8 $H$ をグラフ $G$ の部分グラフとする。このとき
- $G$ が平面的 $\Rightarrow$ $H$ も平面的。
- $H$ が非平面的 $\Rightarrow$ $G$ も非平面的。
証明
(1) $G$ は辺の交差無く描けますので、$H$ はそこからいくつかの頂点と辺を消せば宜しい。
(2) は (1) の対偶です。( 一部分である $H$ すら辺の交差無く描けないのに、 $G$ 全体はムリ、って話。)
※ 辺が多いほど描ける場所が減ってきて、交差ができ易くなる、という感覚が大事です。
$K5$ と $K_{3,3}$
さて、平面性の要
(かなめ)となるのは、次の 2 つのグラフです。
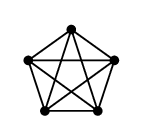 |
|
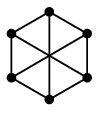 |
$K_5$ |
|
$K_{3,3}$ |
Th.9 $K_5$ は非平面的である。
証明 頑張って辺の交差無く描いてみましょう。
- $K_5$ の部分グラフ $C_5$ はねじらずに描かねばなりません。
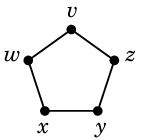
- 辺 $wz$ をこの5角形の内側に描く場合を考えます。(後の Th.14 より内側に描く場合のみ考えればよいことがわかります。)
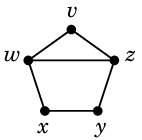
- すると辺 $vx$, $vy$ は5角形の外側に描かざるを得ません
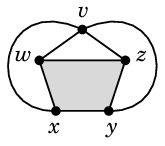 または
または
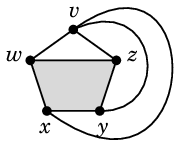 またはその逆
またはその逆
- 残る 2 本の辺 $wy$, $xz$ は色付きの4角形の領域に描かざるを得ませんが、交差させずに描くことは不可能です。
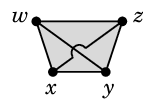
(証明終)
Th.10 $K_{3,3}$ は非平面的である。
証明 Th.9 の証明と同様に、
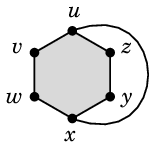
ここまで描くと残る 2 本の辺 $vy$, $wz$ は6角形の内側に描かざるを得ず、
交差させずに描くことは不可能です。
(証明終)
クラトフスキーの定理
Th.11(クラトフスキー) グラフ $G$ について次は同値である。
- $G$ は平面的である。
- $G$ のいかなる部分グラフを縮約しても、$K_5$ や $K_{3,3}$ にはならない。
- $G$ のいかなる部分グラフも、$K_5$ や $K_{3,3}$ に位相同型ではない。
ただし位相同型とは、次の図のように次数 2 の部分を描き替えると同型になること。
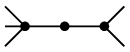 →
→

証明はとても長いので省略します。
Ex.12 ペテルセングラフ は非平面的である。
クラトフスキーの定理を用いた証明は
プリント の第1, 第2の証明を見てください。
Rem.13 Th.11 は定理としては美しいのですが、
「全ての部分グラフ」は膨大な個数存在しますのでプログラミングには使えません。
塩田のグラフ描画ツールでは計算量 $O(n^4)$ の平面性判定アルゴリズムを実装してあります ( $n$ は頂点数 )。




 または
または
 またはその逆
またはその逆


 →
→
