組合せとグラフの理論(塩田)第2回 (6) コンピュータ上でのデータ表現
隣接行列 $A=\left( a_{ij} \right)$
隣接行列とは、グラフの頂点に $V=\{\,v_1,\cdots,v_n\,\}$ と番号を振って
$a_{ij}=(\,v_iv_j$ の形の辺の本数 )
と定めた数を $ij$-成分に持つ行列です。
オーダー $n$ のグラフの隣接行列は $n$ 次の正方行列になります。
Ex.11
$G=$
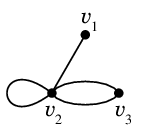
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 2 & 2 \\
0 & 2 & 0 \\
\end{array}
\right).
$
※ 次数の定義と同じく、ループは 1 本で 2 と数えるので $a_{22}=2$ となります。
( 行方向の成分和を次数に一致させるための約束です。)
有向グラフでは
$a_{ij}=(\,v_iv_j$ の形の弧の本数 )
と定めます。
Ex.12
$D=$
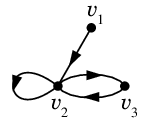
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}
\right).
$
※ 有向グラフでは、ループは 1 本でそのまま 1 と数えます。
隣接リスト
$v_1$ の隣接点のリスト, $v_2$ の隣接点のリスト, $\cdots$, $v_n$ の隣接点のリスト
を並べた二重リストを隣接リストと言います。
Ex.13
$G=$

の隣接リストは
$\{\{\,v_2\,\}, \{\,v_1,v_2,v_3,v_3\,\},\{\,v_2,v_2\,\}\}$.
例えば $v_2$ は $v_1$ との間に辺が 1 本、ループを 1 本、$v_3$ との間に二重辺を持ちますので、
隣接リストの 2 番目の子リストの要素は $v_1,v_2,v_3,v_3$ になります。
Ex.14
$D=$

の隣接リストは
$\{\{\,v_2\,\}, \{\,v_2,v_3\,\},\{\,v_2\,\}\}$.
Ex.15
頂点集合が $V=\{\,1,2,3\,\}$ のとき、隣接リスト
$\{\{\,1,2,3\,\}, \{\,1,3\,\},\{\,1,2\,\}\}$ を持つ無向グラフを描いてみましょう。
まず、$V=\{\,1,2,3\,\}$ から
がわかります。そして
- 1 番目の子リスト $\{\,1,2,3\,\}$ から $1$ はループを 1 本と、$2$, $3$ への辺を持つこと、
- 2 番目の子リスト $\{\,1,3\,\}$ から $2$ は $1$, $3$ への辺を持つこと、
- 3 番目の子リスト $\{\,1,2\,\}$ から $3$ は $1$, $2$ への辺を持つこと
がわかります。よってその絵は
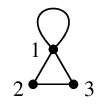
Rem.16
- 辺が多いときは隣接行列が便利
- 辺が少ないときは隣接リストが便利
です。
何故かというと、辺が少ないと隣接行列の要素はほとんど $0$ になるので、
検索に無駄な時間が掛かり、メモリもたくさん必要となるからです。
 の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 2 & 2 \\
0 & 2 & 0 \\
\end{array}
\right).
$
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 2 & 2 \\
0 & 2 & 0 \\
\end{array}
\right).
$
 の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}
\right).
$
の隣接行列は
$A=\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 1 & 1 \\
0 & 1 & 0 \\
\end{array}
\right).
$
