組合せとグラフの理論(塩田)第2回 (5) グラフの同型
グラフの同型
グラフはもののつながりを表す概念なので、「つながり方が同じである」ということを定義しましょう。 (1) による説明:$G$ の右下の頂点を左へ移動させ、下の 2 頂点を右へずらすと $H$ になります。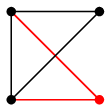 →
→
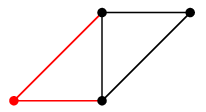 →
→
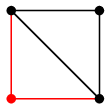
(2) による説明:次のように頂点の名前を付けると、どちらも辺集合が $\{\,12,13,14,23,34\,\}$ になります。
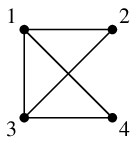 $H=$
$H=$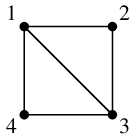
(3) による説明:次のように頂点の名前を付け、 $$\varphi(1)=u,\ \varphi(2)=v,\ \varphi(3)=w,\ \varphi(4)=x$$ と定めると、 隣接していない頂点は $G$ では $2$ と $4$, $H$ では $v=\varphi(2)$ と $x=\varphi(4)$ となって、 $\varphi$ によって隣接関係が写り合っています。
 $H=$
$H=$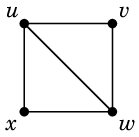
これは次のように頂点番号を振ってもわかりますし(確かめてみましょう)、
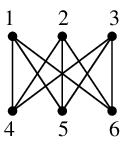 $H=$
$H=$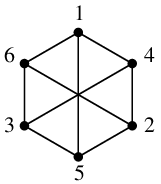
※ 例えば「一筆描きできるか否か」といった、つながり方に関する問題の答えは、同型なグラフであれば同じになります。ここ大事!
証明 動かせば同じ絵になるから。(証明終)
※ しかし、逆は言えません。 オーダー、サイズ、頂点の次数たちが等しいからと言って同型とは限らないのです。 ここめちゃくちゃ大事!
証明 $G$ は三角形を含むが $H$ は含まないから。(証明終)
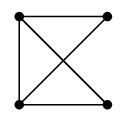 $H=$
$H=$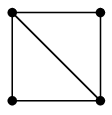
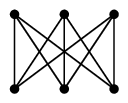 $H=$
$H=$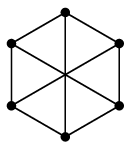
 $H=$
$H=$