組合せとグラフの理論(塩田)第1回 (3) 四色定理
四色定理
グラフ理論を用いて解決した問題をもうひとつ紹介します。
色刷りの地図を作る印刷業者たちは、経験的に次の事実を知っていました:
四色定理 どんな地図でも、4色あれば、隣り合う国同士に違う色を塗って塗り分けることができる。
地図の塗り分けは次のようにしてグラフで表現できます。例えば中部地方周辺の地図を考えましょう。
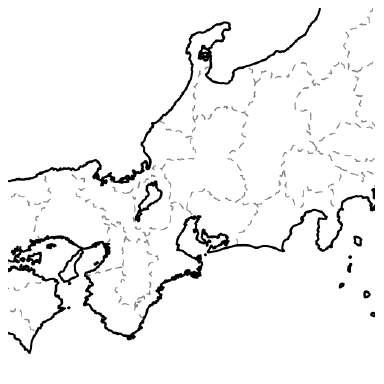
先ず、各都府県にひとつずつ点を描きます。
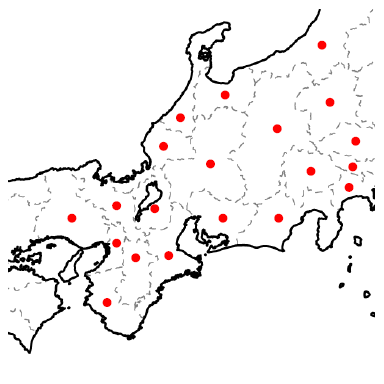
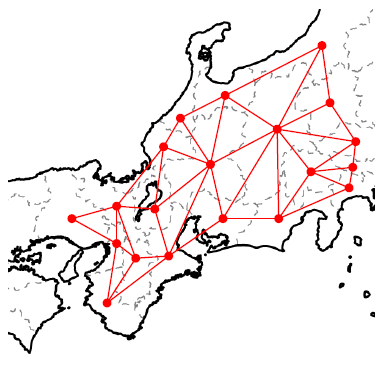
次に、隣り合う都府県について、その点同士を辺で結びます。すると、「隣り合う」というつながりを表現したグラフができます。
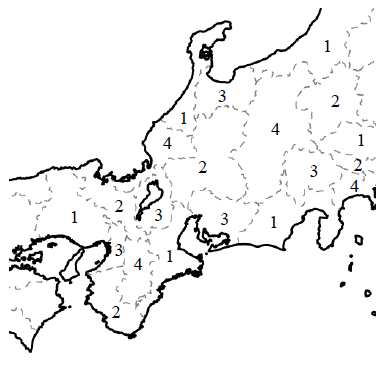
このグラフの点に番号を割り振って、隣り合う点同士の番号が必ず異なるようにします。例えば次のように割り振れば番号は4つで足ります。
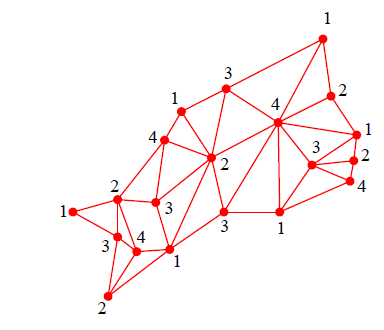
この番号を色の番号だと思って各都府県に色を塗れば、地図の塗り分けができます。
四色問題が学会に提唱されたのは1852年ですが、証明されたのはそれから124年後の1976年。
アッペルとハーケンが「基本的な地図」を約2000個に分類することで解決しました。
コンピュータを用いた証明の魁(さきがけ)でもあります。
フリー素材提供:白地図専門店









